مقاله آموزشی شماره ۶: نوشتار اندیسی

واژه‌های کلیدی

دینامیک سیالات محاسباتی یا CFD، معادلات حاکم بر جریان، اندیس آزاد، اندیس میرا، تانسور، ضرب داخلی، ضرب خارجی، ضرب نقطه‌ای دوگانه

معرفی اندیس‌های میرا و آزاد

حاصل‌ضرب داخلی بردارهای یکه

حاصل‌ضرب خارجی بردارهای یکه

ضرب داخلی دو بردار

ضرب خارجی دو بردار

معرفی تانسور مرتبه 2

پراتورهای دیفرانسیلی روی تانسورها

گرادیان (Gradient)

دیورژانس (Divergence)

کرل (Curl)

ضرب تانسورها و بردارها

جمع‌بندی و نتیجه‌گیری

منابع و مراجع

نوشتار اندیسی یا تانسوری (Tensor Notation) باعث سادگی و اختصار محاسبات در هر دستگاه مختصات می‌شود. بسیاری از کتاب‌ها و مراجع و حتی قسمت Help نرم‌افزارهایی چون فلوئنت بر اساس این نوشتار هستند. قبل از مطالعه معادلات حاکم بر جریان لازم است نوشتار اندیسی فراگرفته شود، زیرا در بسیاری از جملات این معادلات از این نوشتار استفاده می‌شود و بدون این نوشتار فهم قسمت‌های زیادی از معادلات ناقص خواهد بود.

در نوشتار اندیسی در حالت کلی دستگاه مختصات و بردار پایه آن به‌صورت زیر است:

دستگاه مختصات در حالت کلی

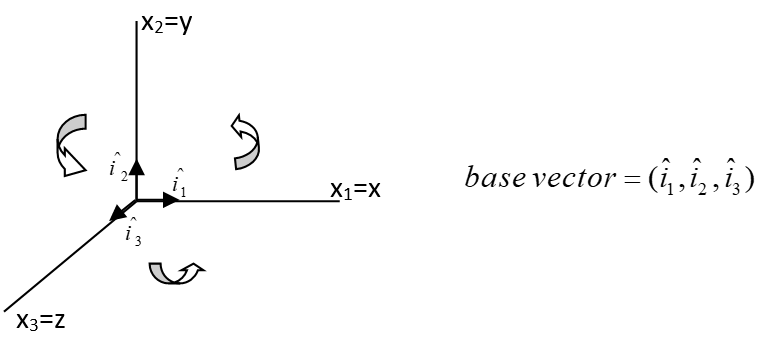
که در مختصات کارتزین:

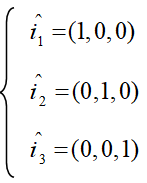
در این نوشتار هر کمیت یک تانسور با مرتبه مشخص است:

• Zero Order Tensor → Scalar → فقط مقدار دارد
• 1^st Order Tensor → Vector → مقدار و یک جهت دارد
• 2^nd Order Tensor → Tensor → مقدار و دو جهت دارد

معرفی اندیس‌های میرا و آزاد

فرض کنید r یک بردار دلخواه مثلا بردار موقعیت باشد:

در عبارت بالا k اندیس میرا (Dummy Index) و معرف جمع است و هر اندیسی غیر آن هم باشد، معنای آن همین خواهد بود:

نشانه این اندیس این است که دو بار در عبارت ظاهر می‌شود. در عبارات بالا معنای ویرگول بین اعداد 1، 2 و 3 «و» است.

در مقابل اندیس میرا اندیس آزاد (Free Index) وجود دارد که یک ‌بار در عبارت ظاهر می‌شود، معرف مؤلفه است و ویرگول بین اعداد 1، 2 و 3 در آن معنای «یا» می‌دهد:

به اندیس میرا Einstein Summation Index هم می‌گویند:

با استفاده از این دو اندیس، مشتق یک کمیت را به‌صورت زیر می‌توان نشان داد:

• اگر P یک کمیت اسکالر باشد، مشتق P در جهت x_k با P_,k‌ نشان داده‌ می‌شود که بسته به k جهت معلوم می‌شود:

• اگر به‌عنوان مثال V بردار سرعت جریان باشد:

حاصل‌ضرب داخلی بردارهای یکه

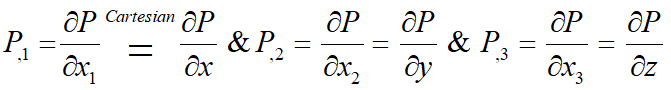
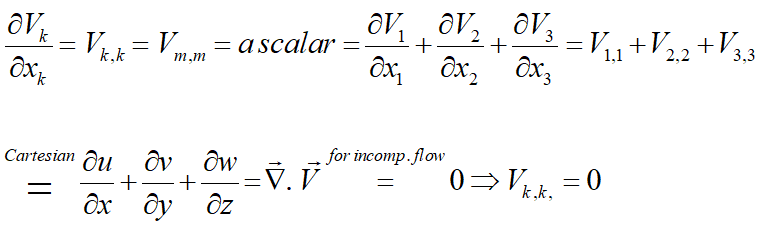
از قبل می‌دانیم:

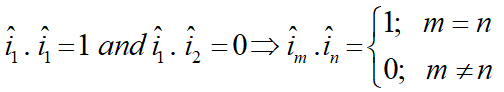
چون n و m هر کدام یک ‌بار تکرار شده‌اند، اندیس آزاد هستند. هر کدام سه مقدار می‌توانند داشته باشند، m, n = 1, 2, 3، بنابراین ضرب داخلی دو بردار یکه 9 جزء یا حالت دارد:

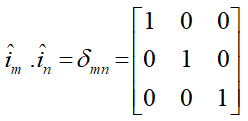
در عبارت بالا δ_mn یک تانسور مرتبه 2 است که Kronecker Delta نام دارد و در حقیقت Unit Tensor است.

مثال: حاصل δ_mnu_n را پیدا کنید.

پاسخ: ابتدا نوع اندیس‌ها را تشخیص می‌دهیم. اندیس m یک ‌بار تکرار شده بنابراین آزاد و اندیس n دو بار تکرار شده است و میرا است.

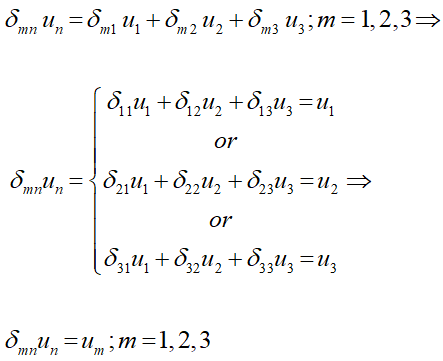
راه‌حل ساده‌تر مثال بالا این است که بگوییم δ_mn تنها در صورتی صفر نیست که m=n باشد، بنابراین در کل عبارت قرار می‌دهیم m=n که باعث می‌شود δ_mm=1.

حاصل‌ضرب خارجی بردارهای یکه

دوباره از قبل می‌دانیم:

در حالت کلی:

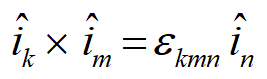
در عبارت بالا اندیس‌های k و m آزاد و اندیس n میرا است. حاصل طبق انتظار یک بردار است، زیرا یک بردار یکه دارد. نام ε_kmn، Paramutation or Alternative Tensor است. این تانسور 3³=27 حالت دارد. برای یافتن مقدار آن از قرارداد زیر استفاده می‌شود:

به‌عنوان مثال:

مثال:

ضرب داخلی دو بردار

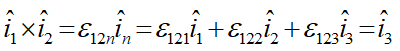
اگر u و v دو بردار دلخواه باشند:

در ادامه به دو روش می‌توان محاسبات را ادامه داد. در روش اول از عبارتی که قبلا اثبات کردیم، استفاده می‌کنیم:

در روش دوم می‌گوییم δ_mn تنها در صورتی صفر نیست که m=n باشد، بنابراین در کل عبارت قرار می‌دهیم m=n که باعث می‌شود δ_mm=1:

در نتیجه:

ضرب خارجی دو بردار

اگر u و v دو بردار دلخواه باشند:

بنابراین حاصل u×v یک بردار است. به‌عنوان مثال مؤلفه اول این بردار می‌شود:

از طرفی از قبل می‌دانیم که ضرب خارجی دو بردار از دترمینان زیر هم قابل محاسبه است:

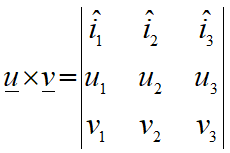
با استفاده از این روش هم مسلما جواب قبلی به دست می‌آید.

مثال: ثابت کنید:

دقت کنید که ضرب بالا به Triple Product معروف و معرف حجمی است که سه بردار A، B و C می‌سازند:

حجم ساخته‌شده توسط سه بردار A، B و C

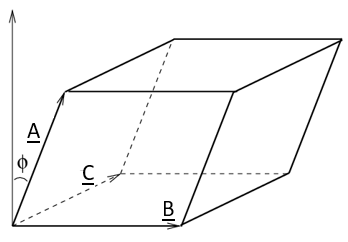
پاسخ:

معرفی تانسور مرتبه 2

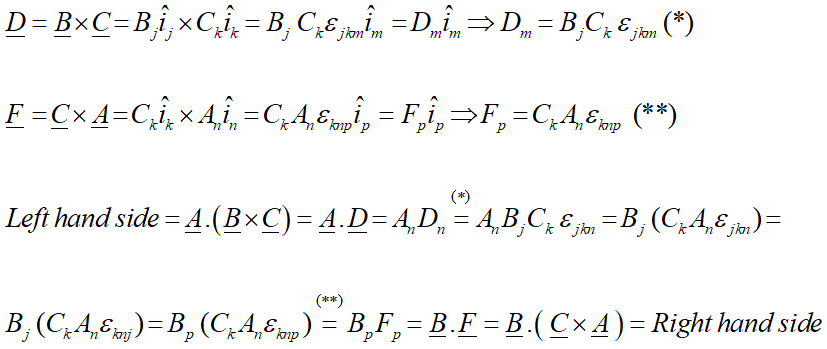
تانسور مرتبه دوم که مؤلفه‌های آن یک ماتریس 3 در 3 تشکیل می‌دهند، از ضرب دیادیک (Dyadic Product) دو بردار حاصل می‌شود:

به ضرب دیادیک ضرب تانسوری (Tensor Product) هم می‌گویند و گاهی اوقات این ضرب را با علامت ⨂ نشان می‌دهند. در این ضرب اندیس‌های آزاد دو بردار در هم ضرب نشده و حفظ می‌شوند. ترتیب هم در این ضرب مهم است:

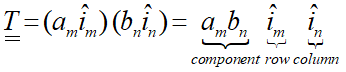
مؤلفه‌های تانسور عبارت‌اند از:

اپراتورهای دیفرانسیلی روی تانسورها

گرادیان (Gradient)

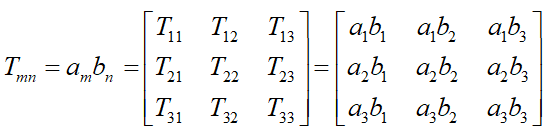
این اپراتور به‌صورت زیر تعریف می‌شود:

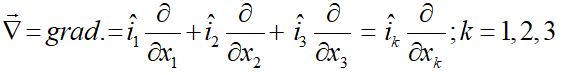
گرادیان یک تانسور مرتبه صفر یا اسکالر یک بردار می‌شود، زیرا:

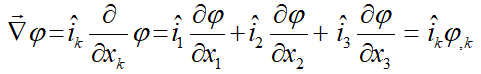
به همین صورت گرادیان یک بردار یک تانسور مرتبه 2 می‌شود:

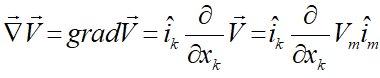
دقت شود که در سیستم مختصات کارتزین، اندازه و جهت بردارهای یکه ثابت است و بنابراین مشتق آن‌ها صفر است. در نتیجه:

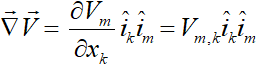
مؤلفه‌های گرادیان بردار سرعت عبارت‌اند از:

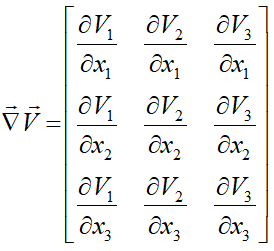
همان‌طور که مشاهده می‌شود، گرادیان یک مرتبه به مرتبه تانسور می‌افزاید.

دیورژانس (Divergence)

این عمل‌گر همان گرادیان است که تنها ضرب داخلی به سمت راست آن اضافه شده است:

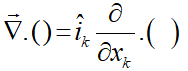
به‌عنوان مثال گرادیان یک بردار به‌صورت زیر است:

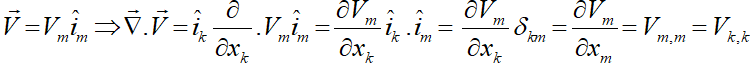
اگر V بردار سرعت در دستگاه کارتزین باشد:

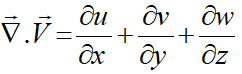
برعکس گرادیان، دیورژانس یک مرتبه از مرتبه‌ی تانسور می‌کاهد. به‌عنوان مثال دیورژانس یک تانسور مرتبه 2 یک بردار می‌شود:

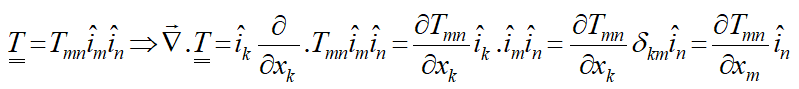
مؤلفه‌های این بردار به‌صورت زیر است:

کرل (Curl)

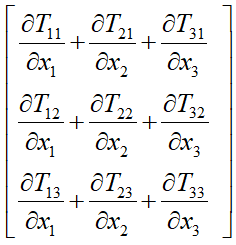
این عمل‌گر همان گرادیان است که تنها ضرب خارجی به سمت راست آن اضافه شده است:

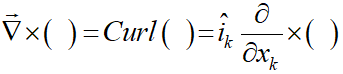
به‌عنوان مثال حاصل کرل یک بردار، یک بردار به‌صورت زیر است:

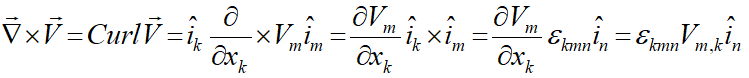
با استفاده از مطالبی که ذکر شد، می‌توان اتحادهای زیر و نمونه‌های مشابه آن را اثبات کرد:

ضرب تانسورها و بردارها

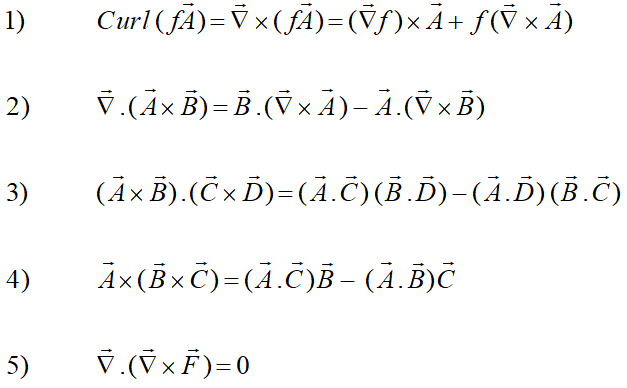
با استفاده از مطالب قسمت‌های قبل می‌توان حالات مختلف ضرب داخلی و خارجی بردارها و تانسورها را انجام داد. به‌عنوان مثال:

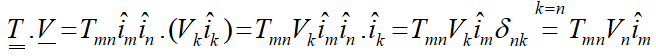
مشاهده می‌شود که حاصل‌ضرب داخلی یک تانسور مرتبه 2 در یک بردار یک بردار می‌شود. ترتیب ضرب مهم است و این ضرب خاصیت جابه‌جایی ندارد.

ضرب داخلی دو تانسور مرتبه 2 به‌صورت زیر است:

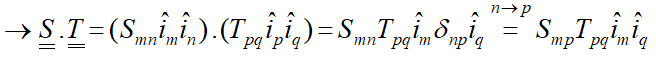
مشاهده می‌شود که نتیجه ضرب داخلی دو تانسور مرتبه 2 یک تانسور مرتبه 2 می‌شود. اگر بخواهیم مشابه ضرب داخلی دو بردار که حاصلش یک اسکالر می‌شود، ضربی داشته باشیم که ضرب دو تانسور مرتبه 2 با آن یک اسکالر شود باید از ضرب نقطه‌ای دوگانه (Double Dot Product) استفاده کنیم:

برای ادامه محاسبه از رابطه گیبس (Gibbs) استفاده می‌شود که به‌صورت زیر است:

در نتیجه:

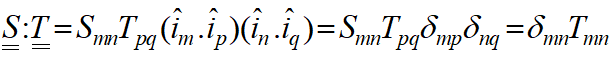
مشاهده می‌شود که حاصل یک اسکالر است. همه 9 مؤلفه نظیر به نظیر در هم ضرب و در انتها جمع می‌شوند.

جمع‌بندی و نتیجه‌گیری

نوشتار اندیسی به‌عنوان لازمه مطالعه و شناخت دقیق معادلات حاکم بر جریان در این مقاله معرفی شد. مفهوم تانسور، ضرب‌های داخلی، خارجی، نقطه‌ای دوگانه و دیادیک به همراه فرم کلی اپراتورهای دیفرانسیلی گرادیان، دیورژانس و کرل در این مقاله مورد بررسی قرار گرفتند. انتظار می‌رود با استفاده از مطالب مورد اشاره در این مقاله بتوانید تفسیر ریاضی درستی از جملات معادلات حاکم داشته باشید.

نظرات خود را در مورد این مقاله با ما در میان بگذارید.

منابع و مراجع