برای مشاهده لیست وارد شوید...
مشاهده محصولات فروشگاههیچ محصولی در سبد خرید نیست.

دینامیک سیالات محاسباتی یا CFD، آشفتگی، Eddy، شبیهسازی، مدلسازی، متوسطگیری زمانی
فهرست مطالب |
همزمان با گسترش استفاده از دینامیک سیالات محاسباتی در صنعت، بحث برخورد با آشفتگی جریان نیز مورد بررسی قرار گرفته است. اهمیت بررسی این موضوع زمانی آشکار میشود که به این نکته توجه شود که خیلی از مسائل کاربردی ماهیت آشفته دارند. بهعنوان مثال جریان در لوله، جریان حول ایرفویل، احتراق و جریان در پاشنده رنگ اکثرا آشفته هستند. بنابراین شناخت مفهوم آشفتگی و برخورد درست با آن میتواند در طراحی نهایی وسیله تاثیر زیادی داشته باشد [۱].
اینکه چه هنگام جریان آشفته است، جواب دقیقی ندارد. معمولا عدد رینولدز جریان را محاسبه و آن را با عدد رینولدز بحرانی مسئله مقایسه میکنند. عدد رینولدز بحرانی عدد رینولدزی است که در آن گذر جریان از آرام به آشفته اتفاق میافتد. در صورت بزرگتر بودن عدد رینولدز جریان از عدد رینولدز بحرانی جریان را آشفته فرض میکنند. اگرچه این روش مرسوم است، ولی اشکالاتی دارد. از جمله اینکه عدد رینولدز بحرانی در بسیاری از مسائل مشخص نیست و تنها میتوان به عدد رینولدز بحرانی مسائل مشابه تکیه کرد. از طرفی اینکه هر جریان با عدد رینولدز بالا را آشفته بدانیم، دقیق نیست. در حقیقت جریان آشفتگی یک سری خواص ذاتی دارد که تنها یکی از آنها عدد رینولدز بالا است. با استفاده از شکل زیر بهصورت تقریبی میتوان در مورد آرام یا آشفته بودن جریان قضاوت کرد:
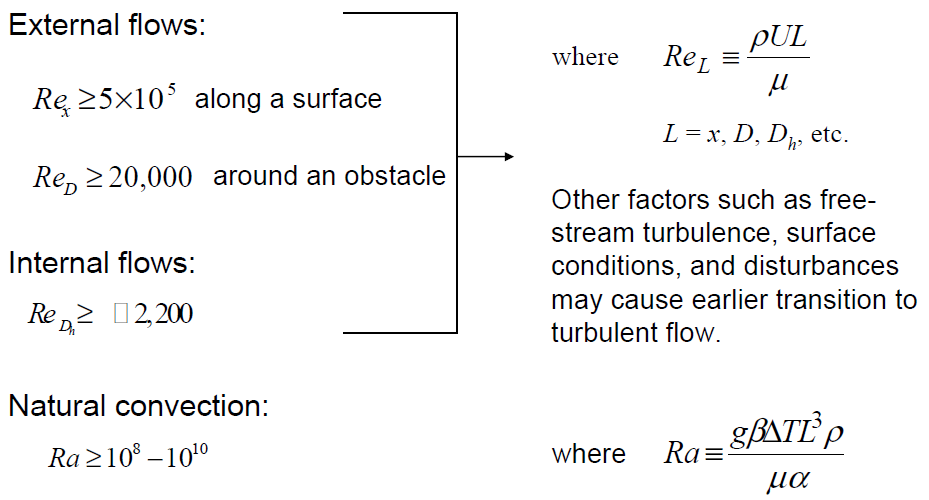
بنابراین میتوان بهصورت کلی گفت که گذر جریان از آرام به آشفته در اعداد رینولدز بین ۲۰۰۰ و ۱e۶ اتفاق میافتد. عدد دقیق رینولدز بحرانی بستگی به ماهیت جریان و مسئله دارد [۲].
تنها در صورتی میتوان یک جریان را آشفته دانست که تمام ویژگیهای زیر در آن جریان حاضر باشند:
∎ تصادفی یا بیقاعده بودن (Randomness or Irregular Nature): به دلیل این ویژگی است که رهیافتی قطعی برای برخورد با آشفتگی وجود ندارد و تنها میتوان به روشهای شرطی یا آماری اعتماد کرد.

∎ Large Diffusive Nature: این خاصیت آشفتگی باعث اختلاط (Mixing) سریع و نرخ انتقال بالای جرم، مومنتم و انرژی میشود. در حقیقت در جریان آشفته نرخ انتقال و اختلاط چند مرتبه بزرگتر از دیفیوژن مولکولی است.
∎ جریان آشفته همیشه در اعداد رینولدز بالا اتفاق میافتد.

∎ آشفتگی یک پدیده پیوسته (Continuum) است و حتی کوچکترین مقیاسهای حرکتی که در جریان آشفته اتفاق میافتد، بزرگتر از هر مقیاس طولی مولکولی است.
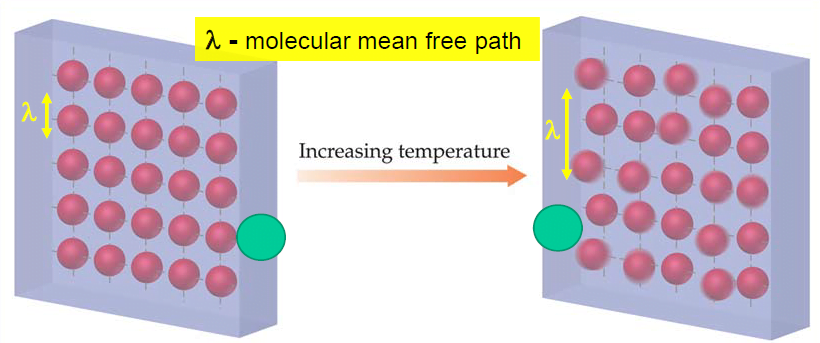
∎ آشفتگی چرخشی و سهبعدی است و در آن نوسانات بزرگ Vorticity وجود دارد.

∎ تمام جریانهای آشفته Dissipative هستند.

∎ جریان آشفته ذاتا ناپایا (Unsteady) است.
در شکلهای زیر تبدیل جریان آرام به آشفته روی یک صفحه تخت نشان داده شده است. عدد رینولدز بحرانی در این حالت تقریبا ۵۰۰ هزار است.
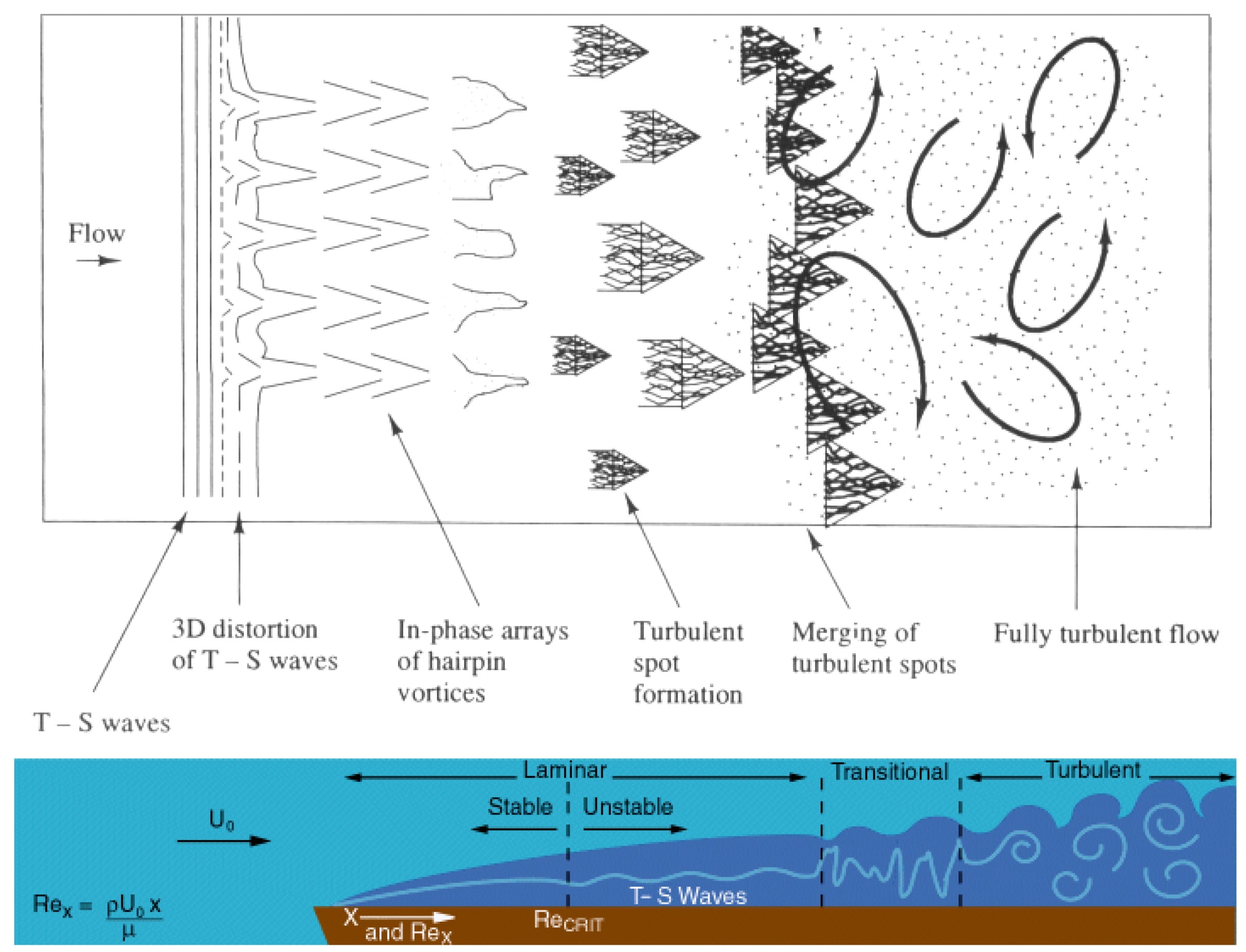


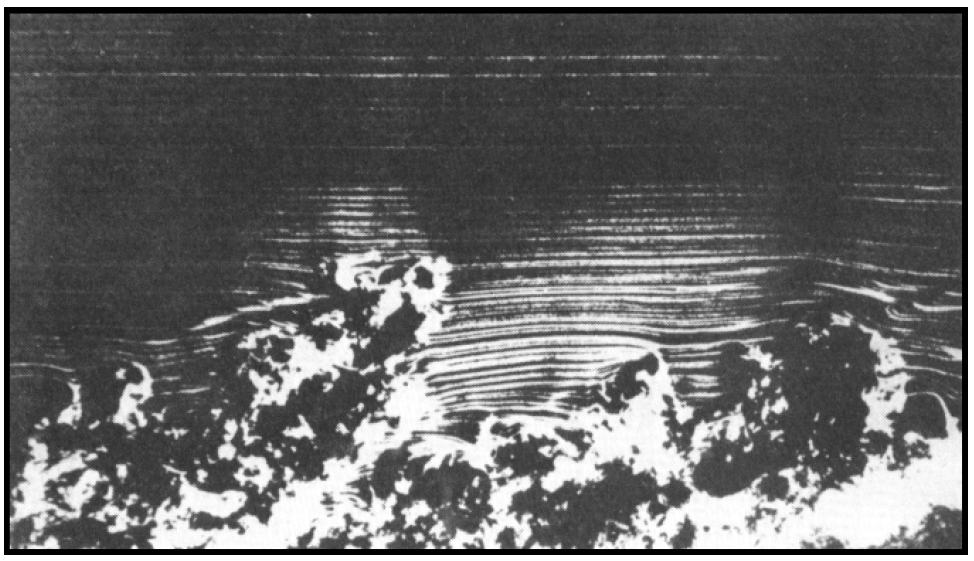
نمونههایی دیگر از تبدیل جریان آرام به آشفته در شکلهای زیر نشان داده شده است.

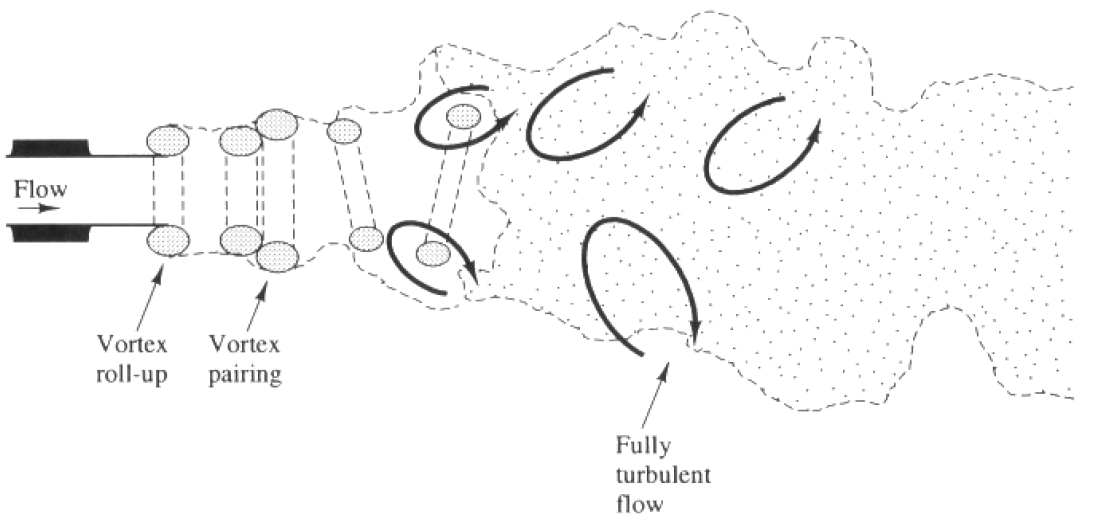
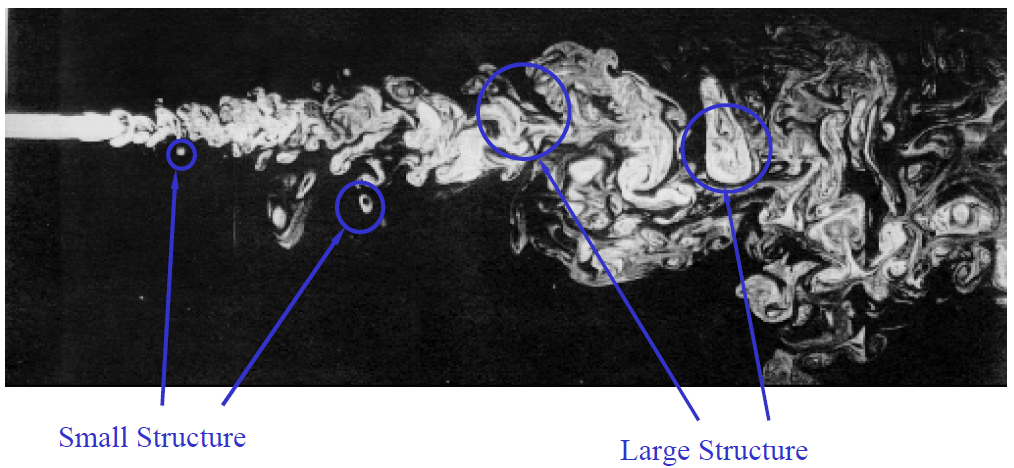

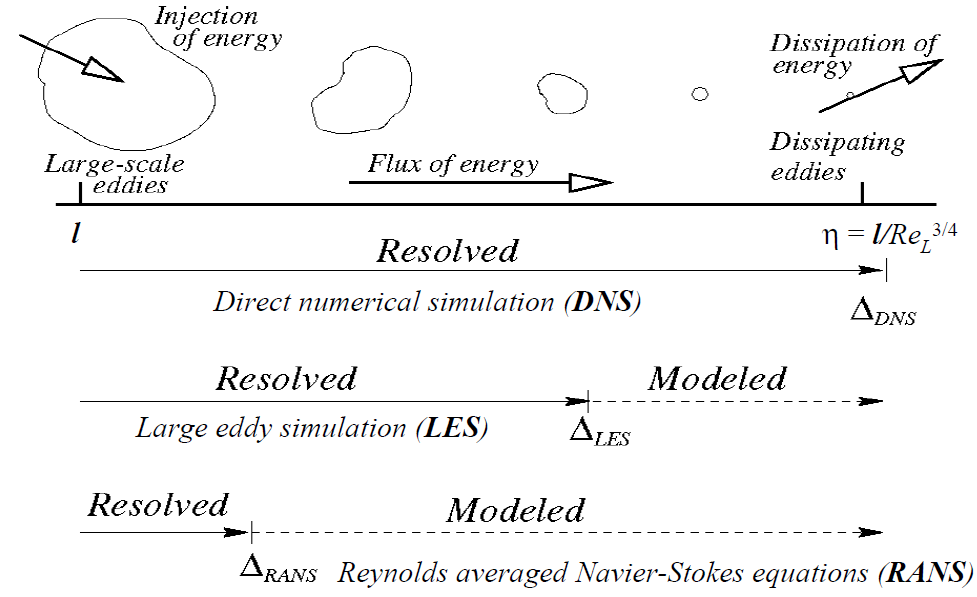
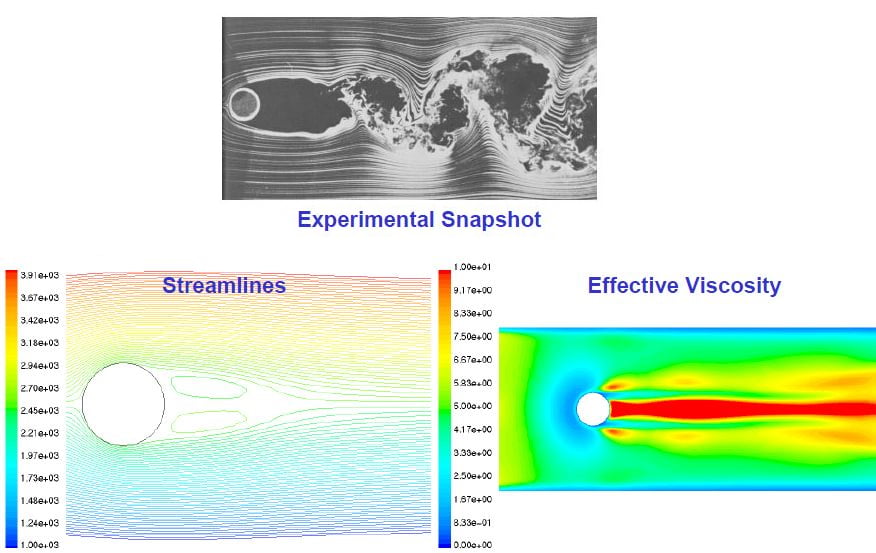
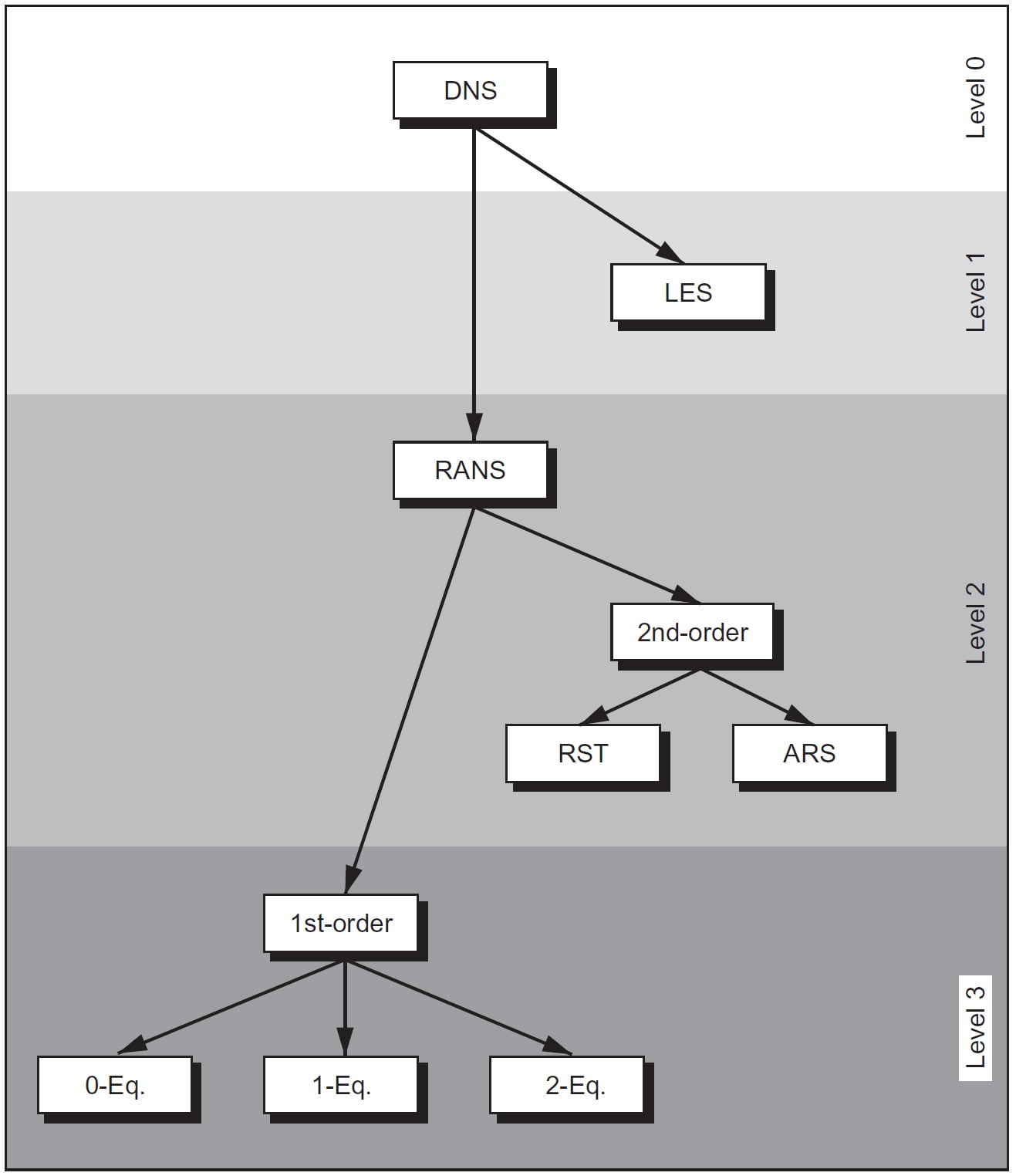
از فیزیک جریان آشفته میدانیم که در جریان آشفته توسعهیافته جزیرههایی به نام ادی (Eddy) با اندازههای مختلف وجود دارد. بر اساس اندازه، ادیها به کوچک، بزرگ و خیلی بزرگ تقسیم میشوند. اندازه کوچکترین ادیها در حد مقیاس کولموگروف (Kolmogorov Length Scale) است و اندازه ادیهای بزرگ و خیلی بزرگ میتواند در حد طول مشخصه جسم باشد. رهیافتهای مختلف عددی برخورد با آشفتگی، بر اساس نحوه رفتار با این ادیها به وجود میآیند. این رهیافتها عبارتاند از:
اولین ایدهای که برای مدلسازی عددی ادیها به ذهن میرسد این است که شبکه محاسباتی را آنقدر ریز کنیم که معادلات گسستهشده مستقیما تمام این ادیها را شبیهسازی کنند. این رهیافت به DNS معروف است. باید توجه داشته باشیم که در صورت استفاده از یک شبکه مناسب که قادر به گرفتن کوچکترین جزئیات جریان باشد، معادلات کامل ناویر-استوکس قادرند هر جریانی را و از جمله جریان آشفته را مدل کنند. بررسیها نشان دادهاند که در عمل این رهیافت فقط برای مسائل ساده با عدد رینولدز پایین قابل استفاده است، زیرا تعداد گرههای شبکه برای تجزیه مکانی میدان حل با استفاده از این رهیافت متناسب با Re9/4 و زمان پردازشگر (CPU-time) متناسب با Re3 است [۳].این زمان بسیار زیاد و شبکه مورد نیاز بسیار بزرگ است و تنها با کامپیوترهای خاص قابل شبیهسازی است. در نتیجه اگرچه رهیافت DNS دقت بسیار بالایی دارد، ولی هزینه محاسباتی آن بسیار زیاد است.
در LES برای حل مشکل DNS شبکه آنقدر ریز میشود که فقط ادیهای با اندازه بزرگ و خیلی بزرگ مستقیما شبیهسازی شوند. بنابراین در این رهیافت میتوان از شبکه درشتتری نسبت به رهیافت DNS استفاده کرد. برای مدلسازی ادیهای کوچک در این رهیافت از مدلهای زیرشبکهای (Subgrid Scale Models) استفاده میشود. باید توجه داشت که در عمل این رهیافت هم به خاطر اینکه بهطور ذاتی سهبعدی و ناپایا است، نیازمند هزینه و زمان محاسباتی زیادی است. البته در سالیان اخیر با پیشرفت قدرت سختافزاری کامپیوترها، استفاده از این رهیافت بیشتر شده است.
در VLES فقط ادیهای خیلی بزرگ مستقیما شبیهسازی میشوند و بنابراین باز هم میتوان از شبکه درشتتری استفاده کرد و ادیهای ریز و بزرگ هم با استفاده از مدلهای زیرشبکهای مدلسازی میشوند. بنابراین از این رهیافت میتوان در مسائل صنعتی بیشتری استفاده کرد، ولی باز هم به نسبت نیازمند یک شبکه ریز خواهد بود. مشاهده میشود هرچقدر وزن شبیهسازی (Simulation) در رهیافت بیشتر باشد، وزن مدلسازی (Modeling) کمتر، دقت بیشتر و زمان و هزینه محاسباتی هم بیشتر میشود.
در RANS با استفاده از میانگینگیری زمانی از معادلات حاکم، تمام ادیها مدلسازی میشوند. در رهیافت ترکیبی از مجموعهای از رهیافتهای ذکرشده استفاده میکنند. در مسائل صنعتی به خاطر صرفهجویی در زمان و هزینه بیشتر از رهیافت RANS استفاده میشود.
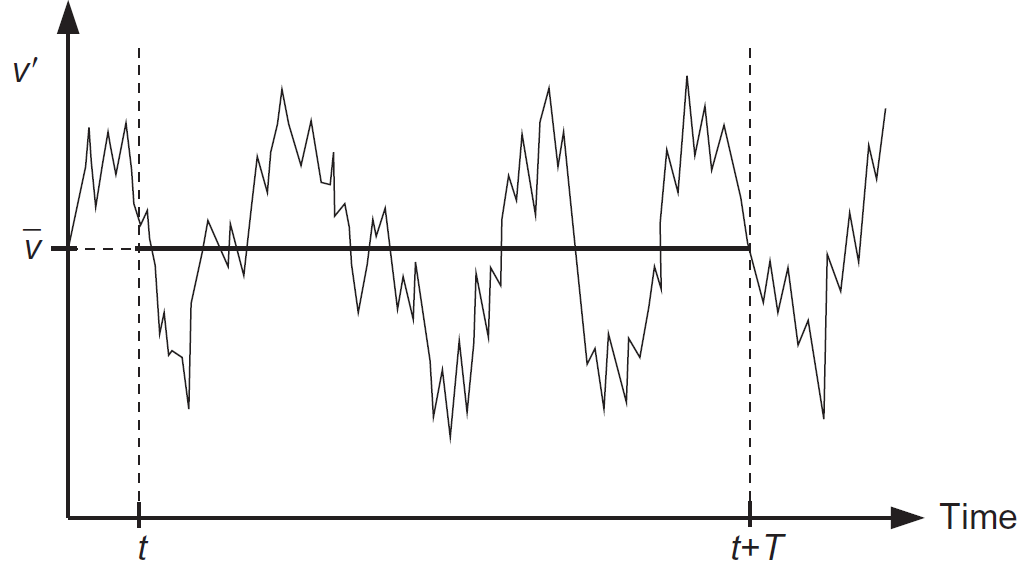
رهیافت RANS که در سال ۱۸۹۵ توسط رینولدز ارائه شد، بر پایه تجزیه متغیرهای جریان به دو قسمت متوسط (Mean Part) و نوسانی (Fluctuating Part) و سپس میانگینگیری از معادلات حاکم است.
![]()
در مواردی که چگالی ثابت نیست، بهتر است که برای مؤلفههای سرعت از تجزیه فاور (Favre Decomposition) که تجزیه با در نظر گرفتن تغییرات چگالی است، استفاده شود. با استفاده از تجزیه فاور معادلات حاکم میانگینگیریشده، به خاطر جملات شامل نوسانات چگالی پیچیده میشوند. بنابراین میتوان از فرض مورکوین (Morkovin’s Hypothesis) استفاده کرد. طبق این فرض ساختار آشفته لایههای مرزی و دنبالهها (Wakes) برای اعداد ماخ زیر ۵ چندان تحت تاثیر نوسانات چگالی قرار نمیگیرد و در نتیجه میتوان میانگینگیری را با فرض ثابت بودن چگالی انجام داد [۳].
با قرار دادن متغیرهای تجزیهشده در معادلات ناویر-استوکس و میانگینگیری از این معادلات، معادلات مشابهی برای کمیتهای متوسط به دست میآید که دو تغییر نیز در آنها روی داده است. یکی ظهور مجهول جدیدی به نام تنشهای رینولدز است:
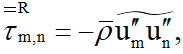
که در آن “um و “un قسمتهای نوسانی مؤلفههای سرعت بر اساس متوسطگیری فاور و علامتهای ˉ و ˜ به ترتیب مربوط به میانگینگیری بر اساس چگالی ثابت و بر اساس چگالی متغیر هستند. تانسور تنشهای رینولدز انتقال مومنتم متوسط به خاطر نوسانات آشفتگی را نشان میدهد. تغییر دیگر ظهور مجهول جدیدی به نام شار حرارتی آشفتگی است:
![]()
بنابراین مشخص است که حل معادلات RANS نیازمند مدل کردن تنشهای رینولدز و شار حرارتی آشفتگی است و بدون این مدلسازی تعداد مجهولات از معادلات بیشتر بوده و معادلات بسته نمیشوند. تا به حال مدلهای آشفتگی زیادی برای بستن معادلات RANS پیشنهاد شده است. این مدلها را میتوان به دو دسته بستن درجه یک (First-order Closure) و بستن درجه دو تقسیم کرد.
مدلهای دسته بستن درجه دو پیچیدهتر و البته انعطافپذیرتر هستند. مدل RST (Reynolds Stress Transport) که ابتدا توسط روتا (Rotta) در سال ۱۹۵۱ پیشنهاد شده است، معادلات انتقال تانسور تنش رینولدز را حل میکند. در این مدل معادلات دیفرانسیل جزئی برای شش تنش رینولدز باید به کمک یک رابطه اضافی بسته شوند. معمولا یک معادله برای نرخ اتلاف آشفتگی بهعنوان رابطه اضافی استفاده میشود. مدلهای RST قادرند تا حد زیادی اثرات غیر محلی و اثرات مربوط به تاریخچه جریان را در نظر بگیرند. همچنین این مدلها قادرند اثرات انحنای خطوط جریان یا چرخش سیستم روی آشفتگی را در شبیهسازی لحاظ کنند.
نزدیکترین مدل به RST مدلهای ARS (Algebraic Reynolds Stress) هستند. این مدلها در واقع ترکیبی از مدلهای سطح پایینتر (از لحاظ دقت) و مدل RST هستند. در مدلهای ARS فقط دو معادله انتقال (بیشتر برای انرژی جنبشی آشفتگی و نرخ اتلاف) استفاده میشود. مؤلفههای تانسور تنش رینولدز بهوسیله معادلات جبری غیرخطی به کمیتهای انتقالی مرتبط میشوند. مدلهای ARS قادر به پیشگویی جریان آشفته چرخشی و جریانهای ثانویه در کانالها با دقتی مشابه مدلهای RST هستند [۳].
به خاطر مشکل Stiffness در مدل RST و مشکل غیر خطی بودن در مدل ARS، در عمل مدلهای مربوط به دسته بستن درجه یک بیشتر مورد استفاده قرار میگیرند. در این مدلها، تنشهای رینولدز با استفاده از فقط یک کمیت عددی به نام لزجت ادی یا لزجت آشفتگی بیان میشوند. این مدلها بر اساس فرض لزجت ادی بوزینس (Boussinesq) هستند. در این فرض مانند جریان آرام، رابطهای خطی بین تنش برشی آشفتگی و نرخ کرنش متوسط در نظر گرفته میشود [۳]. به کمک این فرض برای لحاظ کردن اثرات آشفتگی در معادلات حاکم باید لزجت دینامیکی، μ، در معادلات حاکم با مجموع لزجتهای آرام و آشفته جایگزین شود:
![]()
لزجت آرام را میتوان از رابطه ساترلند (Sutherland) محاسبه کرد. این رابطه برای هوا و در دستگاه SI بهصورت زیر است:
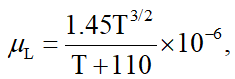
که در آن T برحسب درجه کلوین است.
بهطور مشابه بردار شار حرارتی آشفتگی به این صورت در نظر گرفته میشود:
![]()
که در آن kT ضریب هدایت حرارتی آشفته است. بنابراین علاوه بر ضریب لزجت لازم است که ضریب هدایت حرارتی نیز در معادلات حاکم بهصورت زیر در نظر گرفته شود:
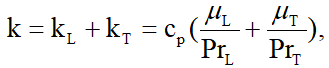
که در آن cp ضریب گرمای ویژه در فشار ثابت و Pr عدد پرانتل (Prandtl) است. عدد پرانتل عموما ثابت در نظر گرفته میشود (برای هوا PrL=0.72 و PrT=0.9). در نهایت ضریب لزجت آشفتگی، μT، باید با استفاده از یک مدل آشفتگی به دست آید تا معادلات RANS بهطور کامل بسته شوند.
مدلهای دسته بستن درجه یک، بسته به تعداد معادله انتقالی که استفاده میکنند، به مدلهای صفر، یک و چند معادلهای تقسیم میشوند. با استفاده از مدلهای صفر معادلهای که به مدلهای جبری نیز مشهورند، لزجت آشفتگی به کمک روابط تجربی که فقط از متغیرهای متوسط محلی استفاده میکنند، محاسبه میشود. بنابراین اثرات مربوط به تاریخچه جریان در این مدلها لحاظ نمیشود و نمیتوانند جریانهای جداشده را بهصورت صحیح مدل کنند. در عوض این مدلها از لحاظ هزینه و زمان محاسبات مقرونبهصرفه هستند. از معروفترین مدلهای این دسته میتوان به مدل بالدوین-لمکس (Baldwin-Lomax) اشاره کرد که در کاربردهای متعددی قدرت خودش را نشان داده است.
تاثیرات تاریخچه جریان را میتوان با به کار بردن مدلهای یک یا دو معادلهای در محاسبات لحاظ کرد. در این معادلات، جابهجایی و پخش آشفتگی با استفاده از معادلات انتقال در نظر گرفته میشود. از مدلهای یک معادلهای معروف میتوان به مدل اسپالارت و آلماراس (Spalart and Allmaras Model) اشاره کرد. همه مدلهای دو معادلهای یکی از معادلات انتقالی که استفاده میکنند، معادله انتقال k، انرژی جنبشی آشفتگی، است. معروفترین مدلهای دو معادلهای مدلهای k-ε و k-ω هستند.
اولین پژوهشها در زمینه رهیافت RANS همانطور که عنوان شد، به تحقیقات رینولدز در سال ۱۸۹۵ در ارتباط با آشفتگی برمیگردد. با این وجود اولین تلاشها برای ارائه یک شرح ریاضی از تنشهای رینولدز به تحقیقات بوزینس در سال ۱۸۷۷ برمیگردد که مفهوم لزجت ادی را ارائه کرد.
با وجود تلاشهایی که رینولدز و بوزینس در زمینه آشفتگی کردند، ولی آنها هیچگاه بهصورت نظاممند به حل معادلات RANS نپرداختند. بنابراین فیزیک آشفتگی همچنان مجهول مانده بود تا اینکه در سال ۱۹۰۴ پرانتل مفهوم لایه مرزی را ارائه کرد. با تمرکز روی آشفتگی پرانتل در سال ۱۹۲۵ مفهوم طول اختلاط (Mixing Length) و بر اساس آن رابطهای برای محاسبه لزجت ادی بر اساس این طول ارائه کرد. این رابطه اساس مدلهای بعدی آشفتگی قرار گرفت.
برای بهبود مدل طول اختلاط و برای واقعیت بخشیدن بیشتر به آن، پرانتل در سال ۱۹۴۵ مدلی را پیشنهاد کرد که در آن لزجت ادی را وابسته به انرژی جنبشی نوسانات آشفتگی، k، میدانست. در این مدل او با استفاده از یک معادله دیفرانسیل، معادله دقیق k را تقریب میزد. با این کار در واقع لزجت آشفتگی وابسته به تاریخچه جریان میشد. با ارائه این مدل خانواده مدلهای آشفتگی یک معادلهای متولد شدند.
مدل آشفتگی کامل خواهد بود، اگر در آن برای به دست آوردن لزجت ادی نیازمند دانستن کمیتی که وابسته به آشفتگی جریان است، نباشیم. بهعنوان مثال اگر برای رسیدن به لزجت ادی نیازمند دانستن اندازه ضخامت مومنتم لایه مرزی باشیم، مدل کامل نخواهد بود، زیرا خود ضخامت مومنتم وابسته به آشفتگی جریان است و مقدار دقیق آن در ابتدا معلوم نیست. کولموگروف (Kolmogrov) در سال ۱۹۴۲ اولین مدل آشفتگی کامل را معرفی کرد. کولموگروف علاوه بر استفاده از معادلهای برای تقریب زدن k، پارامتر ω را بهعنوان نرخ اتلاف انرژی بر واحد حجم و زمان معرفی کرد. در این مدل که معروف به مدل k-ω است، ω هم دارای معادله دیفرانسیلی شبیه به k است. با وجود اینکه این مدل نوید پیشرفت قابل قبولی در آشفتگی را میداد ولی به خاطر محدودیت رایانهها تا ربع قرن بعد از آن عملا استفاده نشد [۴].
با پیشرفت رایانهها در سالهای بعد مدلهای آشفتگی هم پیشرفت زیادی کردند. از جمله، مدلهای جبری توسعه پیدا کردند. ون درایست (Van Driest) در سال ۱۹۵۶ برای مدل طول اختلاط پرانتل، تصحیح میراکننده لزج را پیشنهاد کرد که تا به امروز در تمامی مدلهای جبری استفاده شده است. سبسی و اسمیت (Cebeci and Smith) در سال ۱۹۷۴ مدل طول اختلاط را تا حدی توسعه دادند که میتوان از آن برای خیلی از جریانهای شامل لایه مرزی جدانشده استفاده کرد. برای حذف برخی مشکلات در تعریف مقیاس طولی آشفتگی که در مدل سبسی و اسمیت با استفاده از ضخامت لایه برشی انجام میشد و خود از مجهولات حل بود، بالدوین و لمکس در سال ۱۹۷۸ گونه دیگری از مدل جبری را ارائه کردند که تا به امروز در مسائل زیادی مورد استفاده قرار گرفته است [۴].
برخورد صحیح با آشفتگی از مهمترین اقدامات در هر شبیهسازی CFD است. در این مقاله بعد از معرفی مفهوم آشفتگی، رهیافتهای مختلف برخورد با آشفتگی بیان شدند. با توجه به کاربرد وسیع رهیافت RANS، این رهیافت و تاریخچه آن بهتفصیل بیان شد.
نظرات خود را در مورد این مقاله با ما در میان بگذارید.

با دانلود فایل PDF مقاله همیشه میتوانید به این آموزش دسترسی داشته باشید.
درباره نویسنده: دانشآموخته رشته مهندسی هوافضا از دانشگاه صنعتی شریف، عضو هیئت علمی گروه مهندسی مکانیک در دانشگاه فردوسی مشهد، آموزش و پژوهش در حوزه CFD از سال ۱۳۸۵
توسط جواد سپاهی یونسی
16
اردیبهشتتوسط جواد سپاهی یونسی
16
اردیبهشتتوسط جواد سپاهی یونسی
15
اردیبهشتتوسط جواد سپاهی یونسی
14
اردیبهشتدانلود سریع و آسان
مطالب ما را به راحتی دانلود کنید.اساتید مجرب و حرفهای
تمام مطالب به تایید اساتید کاربلد میرسد.مطالب بهروز
مطالب منطبق بر آخرین ورژن نرمافزارها است.آموزش کاملا فارسی
تمام مطالب آموزشی به فارسی است.پشتیبانی محصولات
تمام محصولات به مدت یک ماه پشتیبانی میشوند.وبسایت CFD EXPERTS با هدف آموزش، مشاوره و انجام پروژه در حوزه CFD راهاندازی شده است. ما قصد داریم به جایگاهی برسیم که بتوانیم پاسخگوی تمام نیازهای محققان و دانشجویان در حوزه CFD باشیم. این مهم نیازمند حمایت شما کاربران عزیز است. قسمتهای جذاب و متنوعی برای CFD EXPERTS در نظر گرفته شده است که به مرور رونمایی خواهند شد. انجام فعالیتهای اصیل، دقیق و با سطح کیفی بالا و همچنین پشتیبانی منظم و مسئولانه محصولات، از مهمترین اهداف CFD EXPERTS است.
تمامی حقوق مادی و معنوی مطالب، مقالات، خودآموزها، دورهها و محصولات برای مدیریت سایت cfdexperts.net محفوظ است و کپیبرداری پیگرد قانونی دارد.
نظرات کاربران