برای مشاهده لیست وارد شوید...
مشاهده محصولات فروشگاههیچ محصولی در سبد خرید نیست.
دینامیک سیالات، معادلات ناویر-استوکس، بقای جرم، بقای مومنتم، بقای انرژی، دیفیوژن، Convection، شار، فرم انتگرالی، فرم دیفرانسیلی، فرم بقایی
فهرست مطالب |
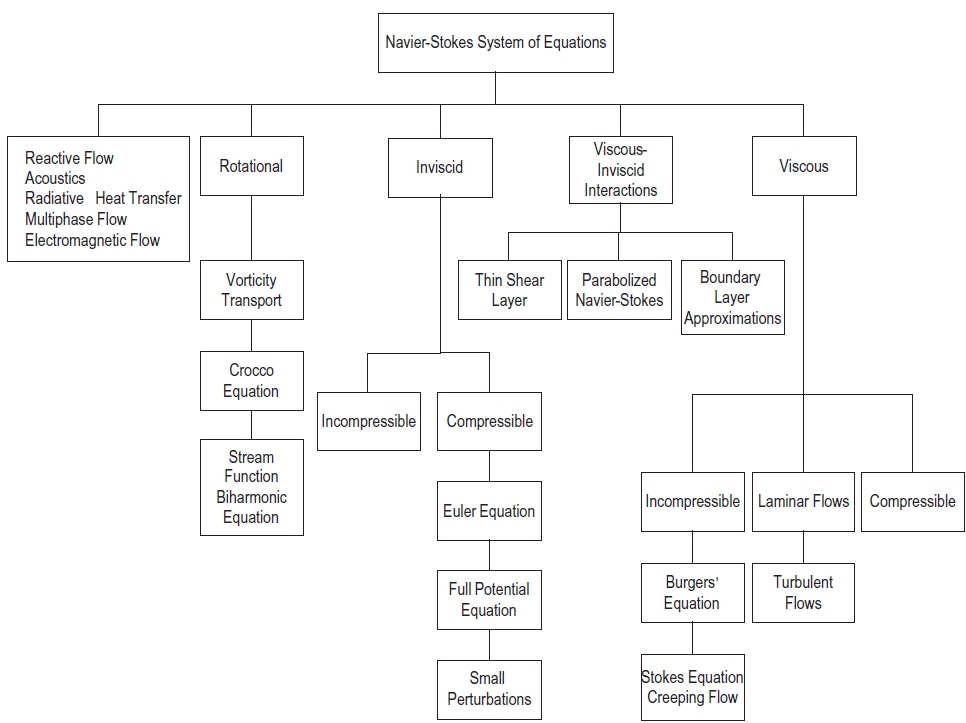
صورتهای سادهشده معادلات ناویر-استوکس
تقریب لایه برشی نازک (Thin Shear Layer Approximation)
معادلات ناویر-استوکس سهموی (Parabolised Navier-Stokes Equations)
معادلات اویلر (Euler Equations)
در CFD معادلات حاکم بر جریان سیال در میدان حل، گسستهسازی و حل میشوند. بنابراین شناخت معادلات حاکم بر سیالات و انتخاب معادلات مناسب برای هر مسئله، از مهمترین مراحل یک شبیهسازی CFD است.
روند حل یک مسئله سیالاتی به این صورت است که ابتدا یک مسئله واقعی پیچیده و ناشناخته وجود دارد. این مسئله سپس ساده و مدل فیزیکی آن ساخته میشود. مدل فیزیکی شامل تعیین کلیات فیزیک مسئله و خصوصیات مرتبط و شرایط حاکم بر آن است. در مرحله بعدی بر اساس مدل فیزیکی و خصوصیات در نظر گرفتهشده در آن، مدل ریاضی که شامل معادلات حاکم به همراه شرایط مرزی و اولیه است، ساخته میشود. مرحله آخر حل معادلات حاکم و رسیدن به نتایج است. برای حل معادلات حاکم بهطورکلی دو روش تحلیلی و عددی وجود دارد. روش تجربی هم برای حل مسئله قابل استفاده است که در آن مستقیما با آزمایش مسئله اصلی نتایج حاصل میشود و با معادلات حاکم سروکار ندارد. برای حل مسائل سیالات، روش مهندسی نیز که ترکیبی از روشهای ذکرشده است، وجود دارد. برای مطالعه بیشتر در مورد روشهای مختلف حل مسائل دینامیک سیالات به این مقاله مراجعه کنید.
قبل از بیان معادلات حاکم بر دینامیک سیالات، لازم است خود واژه دینامیک سیالات بهصورت دقیق معرفی شود. موضوع دینامیک سیالات در حقیقت بررسی حرکت تعاملی تعداد زیادی ذره است. این ذرات مولکول یا اتم هستند. معنی این تعریف این است که چگالی سیال آنقدر زیاد فرض میشود که سیال یک محیط پیوسته (Continuum) تقریب زده میشود. درنتیجه حتی یک المان بسیار کوچک سیال هم آنقدر ذره از سیال دارد که بتوان برای آن سرعت و انرژی جنبشی متوسط، فشار، دما و سایر خواص را تعریف کرد [۱].
معادلات حاکم بر جریان سیال در حالت کلی معادلات ناویر-استوکس (Navier-Stokes) هستند. این معادلات کامل هستند و غیر از فرض پیوستگی سیال، فرض دیگری در آنها اعمال نشده است. این معادلات در حقیقت معادلات بقا (پایستاری) جرم، مومنتم و انرژی هستند. بنابراین خوب است قبل از بیان معادلات حاکم، قانون بقا (Conservation Law) و فرم کلی رابطه آن معرفی شود.
قانون بقا مفهوم اصلی پشت قوانین حاکم بر جریان سال است. این قانون بیان بسیار سادهای دارد. طبق این قانون تغییرات یک کمیت بقایی در داخل یک حجم مشخص از سیال به خاطر تاثیر کلی تعدادی چشمه (Source) داخل آن حجم و عبور آن کمیت از مرزهای حجم است. این کمیت بقایی یک کمیت شدتی (Intensive) مربوط به جریان است و منظور از کمیت عبوری از مرزهای حجم کنترل همان شار (Flux) آن کمیت است که بر حسب خواص ترمودینامیکی و مکانیکی آن سیال قابل تعریف است. شار برای یک کمیت بقایی از جنس بردار و برای یک کمیت برداری از جنس تانسور (Tensor) خواهد بود [۲].
قانون بقا را با یک بیان دیگر به این صورت میتوان معرفی کرد؛ تغییر مقدار کل یک کمیت مانند U در داخل یک دامنه مشخص برابر با توازن بین مقادیر ورودی و خروجی آن کمیت از آن دامنه بهعلاوه مقادیری از آن کمیت است که منابع داخل دامنه تولید یا مصرف میکنند. از آنجا که با جریانی از سیال سروکار داریم، نرخ (Rate) (تغییر زمانی) کمیت U مطرح میشود.
با آنکه U یک کمیت کلی است، باید توجه داشت که لزوما تمام کمیتها و خواص جریان از قانون بقا تبعیت نمیکنند. امروزه مشخص شده است که قوانین کلیای که حرکت جریان سیال را شرح میدهند، قوانین بقای سه کمیت جرم، مومنتم و انرژی هستند [۲]. با توجه به اینکه مومنتم حاصلضرب جرم در سرعت، mV و سرعت یک کمیت برداری است، این قوانین شامل ۵ معادله میشوند.
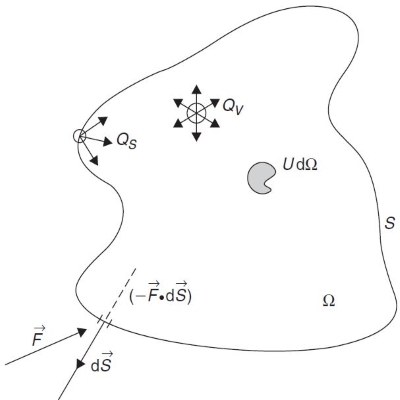
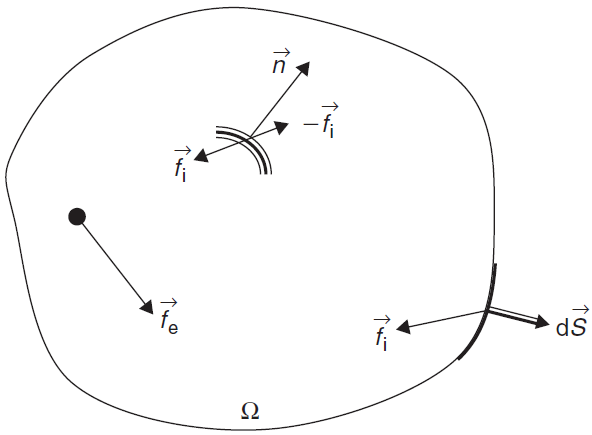
فرض کنید U یک کمیت جریانی اسکالر بر واحد حجم باشد. همچنین فرض کنید Ω یک حجم دلخواه ثابت در فضا و S سطح بسته اطراف آن باشد. به Ω حجم کنترل (Control Volume) و به سطح دلخواه S سطح کنترل (Control Surface) میگویند.
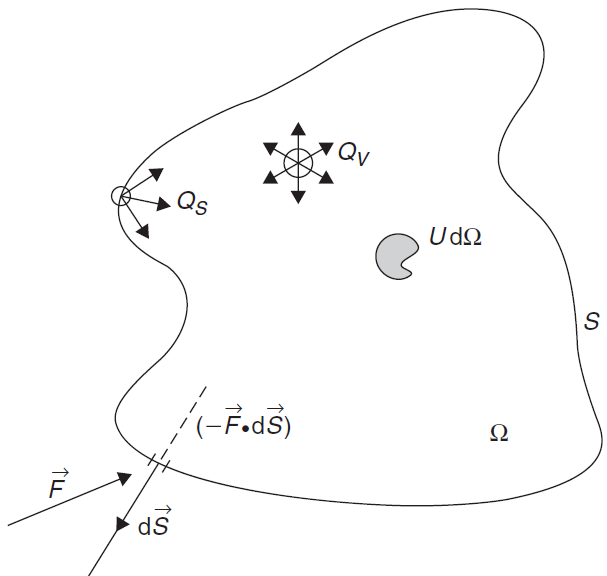
هدف این است که با استفاده از شکل بالا تعریفی که از قانون بقا ارائه شد، به زبان ریاضی بیان شود تا رابطه قانون بقا به دست آید. یکی از عبارات قانون بقا «مقدار کل یک کمیت مانند U در داخل یک دامنه مشخص» است. مقدار کل U داخل Ω عبارت است از:
![]()
بنابراین تغییرات زمانی U میشود:
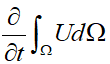
حال عبارت «مقادیر ورودی و خروجی آن کمیت از آن دامنه» به زبان ریاضی ترجمه میشود. این کار با استفاده از مفهوم شار انجام میشود که بیانگر نحوه انتقال کمیت U توسط جریان است. شار بهصورت مقداری از کمیت U که در واحد زمان از واحد سطح عبور میکند، تعریف میشود. طبق این تعریف شار یک مقدار و یک جهت دارد و بنابراین یک کمیت برداری است. شار اگر موازی سطح باشد، چیزی وارد حجم کنترل نخواهد شد. در نتیجه تنها قسمتی از شار که در جهت عمود بر سطح کنترل است، وارد دامنه میشود و در نرخ تغییرات U مشارکت دارد. با این توضیحات طبق شکل بالا، مقداری از کمیت U که در واحد زمان از المان سطح dS عبور میکند، برابر با ضرب داخلی شار در المان موضعی سطح خواهد بود:
![]()
که در آن المان سطح در جهت عمود بر سطح و به طرف بیرون سطح مثبت است [۲].
شار کل برابر با مجموع شار عبوری از المانهای سطح بسته S خواهد بود:
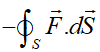
علامت منفی به این خاطر است که شار واردشده به حجم کنترل مثبت در نظر گرفته میشود. وقتی بردار عمود بر سطح به سمت بیرون مثبت فرض شود، ضرب داخلی برای شاری که وارد حجم کنترل میشود، منفی خواهد بود (کسینوس یک زاویه در محدوده ۹۰ تا ۱۸۰ درجه منفی است). بنابراین نیاز به علامت منفی است.
حال سهم منابع یا چشمهها در تغییرات U بررسی میشود. چشمهها به دو دسته سطحی و حجمی تقسیم میشوند و سهم آنها در تغییر U میشود:
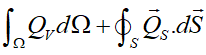
بنابراین فرم کلی قانون بقای کمیت اسکالر U میشود:
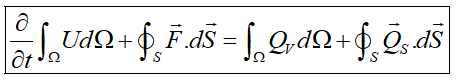
این رابطه که فرم بقایی انتگرالی (Integral Conservative Form) برای یک کمیت اسکالر نامیده میشود، کلیترین فرم رابطه قانون بقا است. دقت شود که این رابطه برای حجم و سطح ثابت برقرار است. همچنین توجه داشته باشید که از آنجا که در رابطه بالا شارها تحت عمل گرادیان یا مشتق نیستند، شارها میتواند ناپیوسته باشند. امواج ضربهای (Shock Waves) یکی از نمونههایی است که شارها در حضور آنها پیوسته نیستند.
با فرض پیوستگی شارها و چشمههای سطحی با اعمال قضیه گاوس (Gauss’ Theorem) در انتگرالهای سطحی، فرم دیفرانسلی قانون بقا به دست میآید. طبق این قضیه انتگرال سطحی شار برابر با انتگرال حجمی دیورژانس شار است:
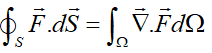
بنابراین:
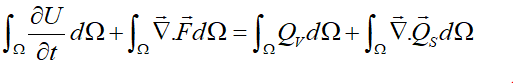
در نتیجه فرم دیفرانسیلی قانون بقای کمیت اسکالر U میشود:
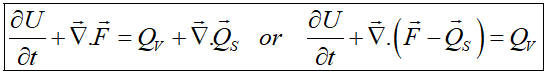
همانطور که روابط نشان میدهند، تاثیر چشمههای سطحی همانند شارها است. بنابراین میشد از اول آنها را بهعنوان شار اضافی در نظر گرفت. ولی جدا نگهداشتن این دو باعث تطابق بیشتر روابط با دیدگاه فیزیکی قانون بقا میشود. در هر صورت عبارت داخل پرانتز میتواند بهعنوان شار موثر (Effective Flux) در نظر گرفته شود. بهعنوان مثال در رابطه بقای مومنتم که بعدا بیان خواهد شد، فشار و تنشهای برشی در حقیقت چشمههای سطحی هستند، ولی معمولا در قالب شار موثر در معادلات میآیند.
دقت کنید که در فرم دیفرانسلی بالا تنها شارها و چشمههای سطحی هستند که تحت عمل گرادیان که مشتق مکانی است، هستند. فرم دیفرانسیلی میتواند بقایی (Conservative) یا غیربقایی (Non-Conservative) باشد. اگر تمام جملات مشتق مکانی تنها در یک عملگر دیورژانس جمع شوند، آن فرم بقایی و در غیر این صورت آن فرم غیربقایی یا شبهخطی (quasi-linear) خواهد بود.
فرم دیفرانسیلی محدودیت بیشتری نسبت به فرم انتگرالی دارد، زیرا در آن شارها باید مشتقپذیر باشند که بهعنوان مثال در حضور امواج ضربهای مشتقپذیر نیستند.
در قسمت قبل در مورد ماهیت و نحوه محاسبه شار هر کمیت صحبت نشد. وجود شار برای یک کمیت دو دلیل و منبع دارد؛ یکی انتقال Convective سیال (حرکت سیال با سرعت مشخص) و دیگری تلاطم مولکولی سیال که این مورد حتی برای سیال ساکن هم وجود دارد. مورد اول شار Convective نامیده میشود و معرف میزانی از U است که توسط جریان منتقل یا حمل میشود:
![]()
شار Convective عبوری از المان سطح عبارت است از
![]()
که معنای فیزیکی مهمی در سیالات دارد. بهعنوان مثال اگر U چگالی سیال باشد، شار Convective متناظر آن که از المان سطح dS عبور میکند، نرخ دبی جرمی است:
![]()
این کمیت در حقیقت بیانگر میزان جرم عبوری از المان dS بر واحد زمان است که بر حسب kg/s بیان میشود.
اگر U برابر ρu باشد، از آنجا که قبلا گفته شد U یک کمیت جریانی بر واحد حجم است، بنابراین u یک کمیت جریانی بر واحد جرم خواهد بود. در این صورت شار Convective میشود:
![]()
عبارت بالا بهصورت واضح معنای فیزیکی شار Convective را نشان میدهد، زیرا نشاندهنده میزانی از کمیت u است که توسط دبی جرمی محلی حمل میشود [۲].
قسمت دوم شار، شار Diffusive است که در سیال در حال سکون هم حضور دارد و به خاطر اثر ماکروسکوپیک (Macroscopic) تلاطم حرارتی مولکولی است. اختلاف در شدت یک کمیت باعث انتقال در فضا بهمنظور کاهش ناهمگونی در سیال میشود، زیرا سیال با حرکت مولکولی تمایل به تعادل و یکنواختی دارد. این شار متناسب با گرادیان کمیت است. برای یک سیال همگن این گرادیان صفر است.
شار Diffusive ممکن است همیشه وجود نداشته باشد. بهعنوان مثال در یک سیال تکفاز ساکن دیفیوژن (Diffusion) جرم مخصوص وجود ندارد، زیرا هر جابهجایی جرم مخصوص معرف یک جابهجایی ماکروسکوپیک در ذرات سیال خواهد بود. به همین دلیل است که در رابطه بقای جرم، شار Diffusive وجود ندارد.
پدیده دیفیوژن در کل متفاوت از Convection است. برای فهم فیزیکی دیفیوژن مثالی ذکر میشود. مخزن آبی را در حالت سکون در نظر بگیرید که قطرهای رنگ سیاه به داخل آن تزریق میشود. چگالی رنگ را برابر با چگالی آب فرض کنید. آیا قطره سر جای خودش خواهد ماند؟ قطعا خیر. بعد از گذشت زمانی معین همه مخزن رنگی خواهد شد.
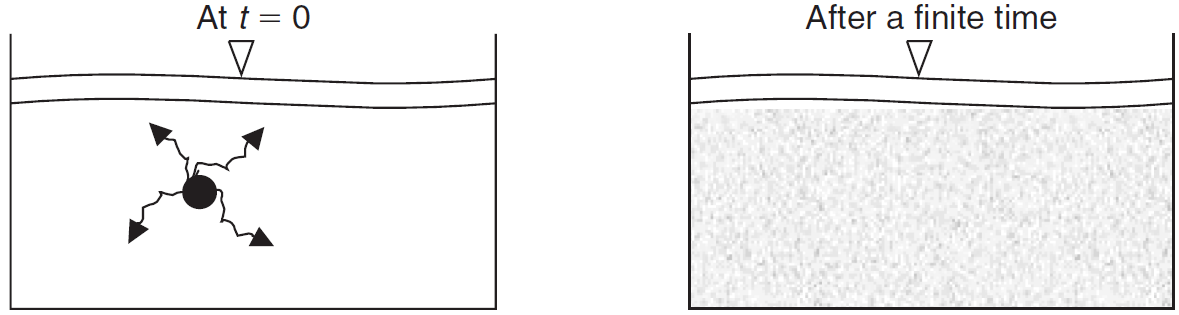
آب هیچ جریان یا سرعتی نداشته ولی رنگ در کل مخزن پخش شده است. چه اتفاقی افتاده است؟ به خاطر تلاطم مولکولی، مولکولهای رنگ مدام در حال برخورد با مولکولهای آب هستند و به آنها ضربه میزنند تا در نهایت در یک نقطه دلخواه آرام گیرند. در نتیجه بعد از گذشت زمان مشخصی مولکولهای رنگ همه جا داخل مخزن حضور خواهند داشت. ناظر بیرونی مولکولها را نمیبیند، ولی نتیجه ماکروسکوپیک برخورد مولکولی برایش قابل مشاهده است.
پدیدهای که در این مثال اتفاق میافتد، دیفیوژن و دلیل آن گرادیان غلظت رنگ است. تا وقتی که این گرادیان وجود داشته باشد، دیفیوژن اتفاق میافتد. در حقیقت دیفیوژن متناسب با گرادیان غلظت است. دیفیوژن متضاد با گرادیان است و تمایل به یکنواختی دارد. این تناسب یک ضریب به نام ضریب پخش (Diffusivity Coefficient) دارد که مقدار آن وابسته به کمیت و محیط است. همه این موارد ذکرشده به زبان ریاضی در قانون Fick (Law of Fick) خلاصه شده است:
![]()
که در آن κ ثابت تناسب و در حقیقت ضریب پخش و واحد آن برای هر U دلخواه m2/s است. با این تفاسیر فرم دیفرانسیلی قانون بقا بهصورت زیر درمیآید:
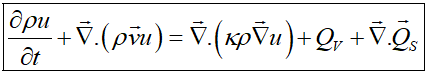
رابطه بالا فرم بقایی معادله انتقال کمیت U=ρu است و معادله Convection–Diffusion نیز نامیده میشود. ساختار این معادله چه از منظر فیزیکی و چه از منظر ریاضی بسیار مهم است، زیرا در حقیقت ستون فقرات مدلسازی ریاضی تمام پدیدههای سیالاتی است.
شارهای Convective و Diffusive از منظر فیزیکی تفاوتهای زیر را با هم دارند:
تفاوتهای بین Convection و Diffusion در جدول زیر بهصورت خلاصه ذکر شده است. این تفاوتها نه تنها از لحاظ درک فیزیکی مهم هستند، بلکه از نظر روشهای CFD و انتخاب نحوه گسستهسازی این جملات مهم هستند، زیرا به قول معروف:
The scheme must follow the physics.
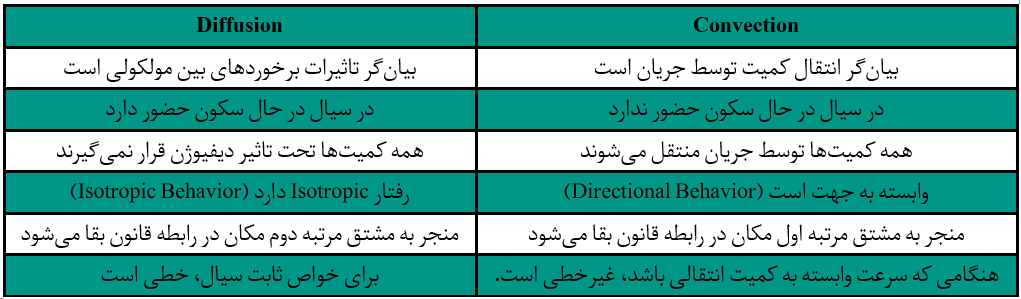
با استفاده از عدد پکلت میتوان در مورد برتری و غالب بودن دیفیوژن یا Convection در هر مسئله قضاوت کرد:
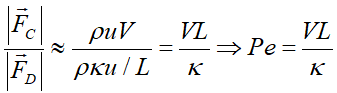
که در آن V سرعت مرجع و L طول مرجع است. همانطور که مشاهده میشود، عدد پکلت تقریبا نسبت Convection به دیفیوژن است. بنابراین اگر عدد پکلت بسیار بزرگتر از یک باشد، تغییرات کمیت U غالبا توسط Convection حاصل میشود و اگر کمتر از یک باشد، این دیفیوژن است که تاثیر بیشتری در تغییرات کمیت U دارد [۲].
در قسمتهای قبلی کمیت مورد بررسی اسکالر بود. اگر این کمیت برداری باشد، شار از جنس تانسور، چشمه حجمی از جنس بردار و چشمه سطحی از جنس تانسور میشود. در این حالت فرم انتگرالی قانون بقا برای یک کمیت برداری به این صورت خواهد بود:
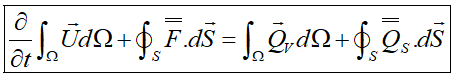
با اعمال قضیه گرین با فرض پیوستگی شارها و چشمههای سطحی:
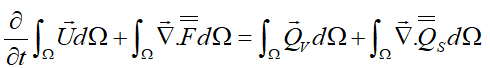
بنابراین فرم دیفرانسیلی قانون بقا برای یک کمیت برداری بهصورت زیر خواهد بود:
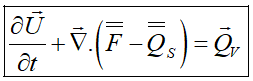
فرم بالا بقایی است، زیرا تمام جملات شار مکانی تحت عمل یک دیورژانس هستند.
دقت داشته باشید که گرادیانِ یک تانسور مرتبه ۲، یک بردار میشود. قسمت Convective تانسور شار با استفاده از رابطه زیر به دست میآید:
![]()
ضرب سمت راست رابطه بالا ضرب دیادیک (Dyadic Product) بردارها است. در نوشتار اندیسی رابطه بالا بهصورت زیر است:
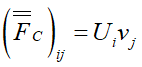
که نشاندهنده مولفههای شار Convective بر حسب مولفههای بردارهای U و v است. قسمت Diffusive تانسور شار برای یک سیستم همگون بهصورت زیر است:
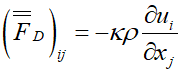
و نیز
![]()
همانطور که ذکر شد، معادلات حاکم بر جریان سیال همان معادلات بقای جرم، مومنتم و انرژی هستند. نکته جالب این معادلات این است که هر جریانی با هر پیچیدگی و شرایطی که وجود داشته باشد، معادلات حاکم بر آن همین معادلات هستند. بقای مومنتم همان قانون دوم نیوتن و بقای انرژی همان قانون اول ترمودینامیک است.
برای این قانون بقا:
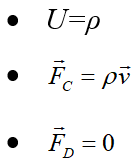
بنابراین در غیاب چشمههای جرمی، فرمهای انتگرالی و دیفرانسیلی رابطه بقای جرم بهصورت زیر خواهند بود:
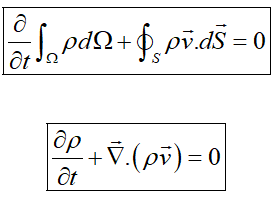
با اعمال دیورژانس:
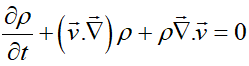
با معرفی مشتق مادی یا مشتق کلی (Material or Total Derivative):
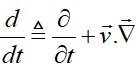
فرم دیگر قانون بقای جرم بهصورت زیر خواهد بود:
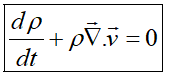
با آنکه از لحاظ ریاضی هر دو فرم دیفرانسیلی کاملا یکسان هستند، ولی از منظر CFD و از لحاظ گسستهسازی عددی لزوما یکسان نیستند. فرم اول بقایی ولی فرم دوم غیربقایی یا غیرخطی است.
دقت کنید که در دستگاه کارتزین:
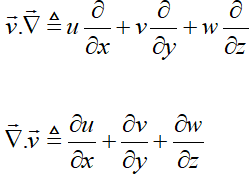
مومنتم یک کمیت برداری و برابر با حاصلضرب جرم در سرعت است، بنابراین:
مورد آخر به این دلیل است که فرض میشود برای یک سیال در حال سکون دیفیوژن مومنتم وجود ندارد. حال باید چشمههایی که باعث تغییر مومنتم میشوند، مشخص شوند. طبق قانون نیوتن این چشمهها نیروهای وارده بر سیستم هستند که شامل نیروهای حجمی خارجی (fe) و نیروهای داخلی (fi) بر واحد جرم میشوند. در نتیجه بردار Qv در قانون بقا شامل مجموع نیروهای حجمی خارجی بر واحد حجم (ρfe) و مجموع تمام نیروهای داخلی(ρfi) میشود.
نیروهای داخلی مربوط به تغییر شکل المانهای سیال میشوند. چون تغییر شکل المان سیال ممکن است، پس نیرویی پشت این تغییر شکل وجود دارد که همان نیروی داخلی است. بر اساس قانون عمل و عکسالعمل، اثر کلی نیروهای داخلی وقتی در تمام نقاط داخل دامنه در نظر گرفته شوند، صفر است و تنها روی نقاط سطحی است که اثر این نیروها باقی میماند. در نتیجه چشمههای سطحی در فرم کلی قانون بقا، در این حالت همان نیروهای داخلی با شدت زیر هستند.
![]()
تانسور تنش داخلی یک خاصیت موضعی سیال است. با فرض سیال نیوتنی (سیالی که در آن تنشهای لزج بهصورت خطی تابع نرخ کرنش باشند):
![]()
که در آن I تانسور واحد (Unit Tensor)، pI ترم فشار Isotropic و τ تانسور تنش برشی لزج است:
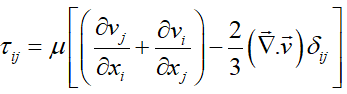
این رابطه برای یک سیال نیوتنی که در تعادل ترمودینامیکی قرار دارد، برقرار است. حالت کلیتر رابطه بالا بهصورت زیر است:
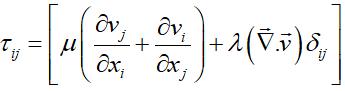
که در آن λ ضریب دوم لزجت است و جز در موارد خاص (دما و فشارهای بسیار زیاد):
![]()
لازم است توجه شود که تنش برشی لزج در حقیقت همان نیروی اصطکاک داخلی بین لایههای سیال است.
با استفاده از فرم انتگرالی رابطه بقای یک کمیت برداری، رابطه بقای مومنتم بهصورت زیر درمیآید:
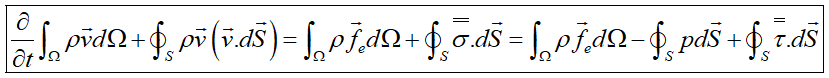
با اعمال قضیه گرین:
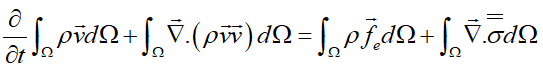
بنابراین فرم دیفرانسیلی رابطه بقای مومنتم بهصورت زیر خواهد بود:
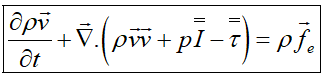
اگر از سمت چپ رابطه بالا، رابطه بقای جرم که درضرب شده است، کم شود، فرم غیربقایی رابطه بالا میشود:
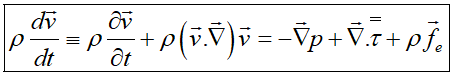
با فرض ثابت بودن ضرایب لزجت میتوان اثبات کرد:
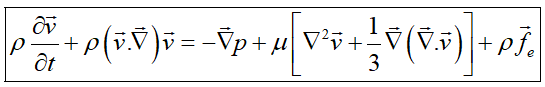
اگر علاوه بر آن فرض تراکمناپذیری سیال شود:
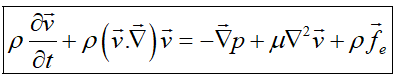
اگر علاوه بر فرضیات قبلی فرض غیرلزج شود:
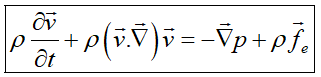
که به معادله اویلر (Euler) معروف است.
دقت شود که ترم Convection غیرخطی است. همچنین جمله شامل تنش برشی(τ.∇) تمام خواص شار دیفیوژن را دارد. در حقیقت تنشهای لزج نقش دیفیوژن را دارند و ضریب لزجت سینماتیکی معادل ضریب دیفیوژن و واحد آن m2/s است.
نسبت بین Convection و دیفیوژن مومنتم همان عدد رینولدز است که فرم خاصی از عدد پکلت با لزجت سینماتیکی بهعنوان ضریب دیفیوژن است:
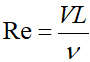
از منظر ترمودینامیک محتوای انرژی یک سیستم توسط انرژی داخلی (Internal Energy) بر واحد جرم آن سنجیده میشود. در سیالات، کمیت بقایی انرژی کل (Total Energy) است که بهصورت مجموع انرژی داخلی و انرژی جنبشی بر واحد جرم تعریف میشود:
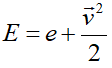
E انرژی کل بر واحد جرم است، بنابراین ρE بر واحد حجم خواهد بود. بنابراین برای قانون بقای انرژی:
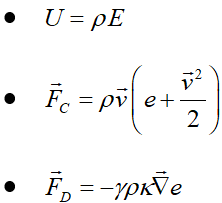
عبارت آخر به این دلیل است که طبق تعریف، شار Diffusive به خاطر حرکت سیال وجود ندارد. ضریب κ ضریب Thermal Diffusivity و γ نسبت ضرایب گرمای مخصوص در فشار و دمای ثابت است، γ=cp/cv.
طبق قانون اول ترمودینامیک منابع یا چشمههایی که میتوانند انرژی کل سیستم را تغییر دهند، کار نیروهای وارده بر سیستم و گرمای منتقلشده به سیستم است. در واقع شار Diffusive دیفیوژن حرارت را در یک سیال ساکن به خاطر هدایت (Conduction) مولکولی نشان میدهد. در حالت کلی این شار منطبق بر قانون فوریه برای انتقال حرارت هدایت (Fourier’s Law of Heat Conduction) نوشته میشود:
![]()
که در آن k ضریب هدایت حرارتی است و داریم:
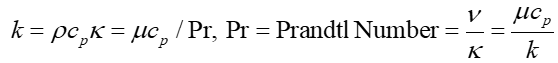
در ارتباط با چشمههایی که عامل تغییر انرژی سیال هستند، باید بین چشمههای سطحی و حجمی تمایز قائل شد. چشمههای حجمی مجموع کار نیروهای حجمی و چشمههای حرارتی غیر از هدایت مانند تشعشع و انرژی آزادشده از واکنش شیمیایی است که با qH نشان داده میشوند. در نتیجه در واحد حجم:
![]()
چشمههای سطحی در نتیجه کاری است که توسط تنشهای برشی داخلی وارده بر سطوح حجم کنترل روی سیال انجام میشود، با فرض عدم وجود چشمههای حرارتی سطحی خارجی:
![]()
بنابراین فرمهای انتگرالی و دیفرانسیلی رابطه بقای انرژی بهصورت زیر خواهند بود:
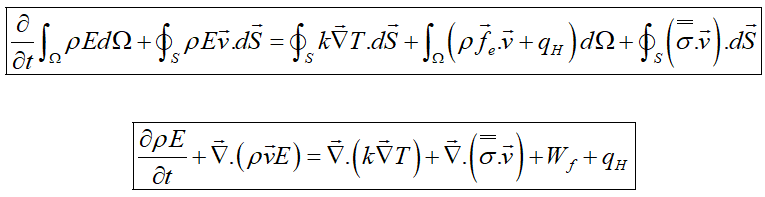
که در آن Wf کار نیروهای حجمی خارجی است:
![]()
با باز کردن جمله زیر
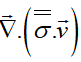
و استفاده از تعریف انتالپی بهصورت h=e+p/ρ، فرم دیفرانسیلی بالا بهصورت زیر درمیآید:
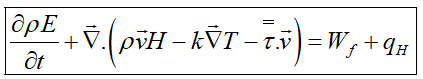
که در آن H انتالپی کل یا سکون است:
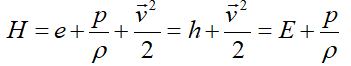


مرجع [۱] معادلات ناویر-استوکس را که در حقیقت یک دستگاه معادلات PDE غیرخطی کوپل هستند، بهصورت زیر جمعبندی کرده است:
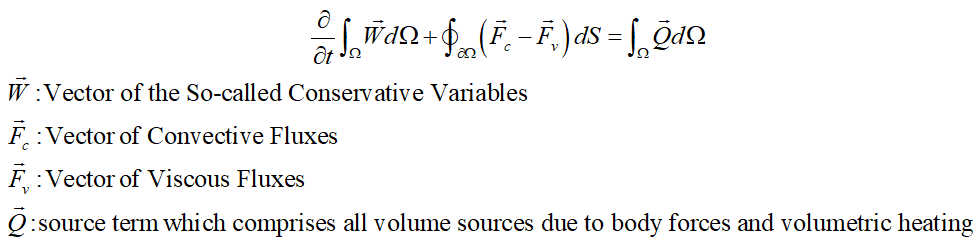
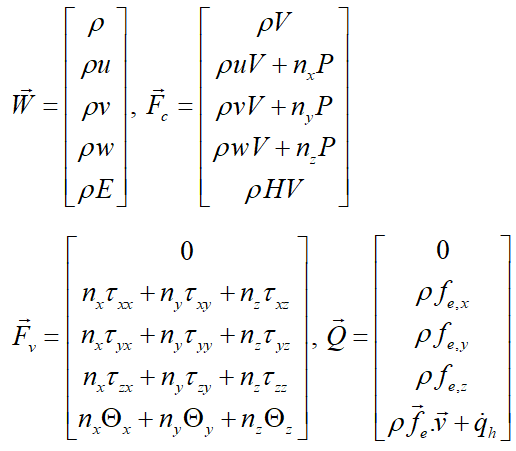
در روابط بالا Vسرعت عمود بر المان سطح dS است که بهصورت حاصلضرب داخلی بردار سرعت در بردار یکه عمود بر سطح تعریف میشود:
![]()
همچنین H آنتالپی کل و E انرژی داخلی کل است:
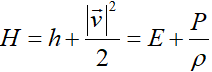
علاوه بر آن جملات شامل کار تنشهای لزج و انتقال حرارت جابهجایی بهصورت زیر هستند:
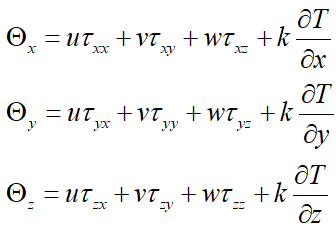
باید دقت کرد که روابط بالا برای سیال نیوتنی و حجم کنترل ثابت در فضا هستند.
برای حل یک مسئله سیالاتی، این معادلات باید با شرایط مرزی (Boundary Conditions) و شرایط اولیه (Initial Conditions) مناسب حل شوند. تاکنون ریاضیات قادر به حل این معادلات بهصورت تحلیلی نبوده، مگر اینکه فرضیات و سادهسازیهای زیادی در آنها اعمال شود. در CFD این معادلات در شبکهای از گرهها (سلولها) گسستهسازی و حل میشوند.
دستگاه معادلات بالا شامل ۵ معادله برای ۵ متغیر بقایی (Conservative Variable) ρ، ρu، ρv، ρw و ρE است، اما تعداد مجهولات ۷ است (ρ، u، v، w، E، P و T). بنابراین برای حل این دستگاه نیاز به دو معادله کمکی مانند معادله حالت گاز ایدهآل و رابطه آنتالپی با دما است:
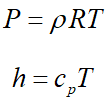
در برخی حالات که مسئله واقعی ذاتا سادگیهایی دارد، میتوان صورتهای سادهتری از معادلات ناویر-استوکس را استفاده کرد که در این قسمت اجمالا معرفی میشوند.
اگر مسئله مورد بررسی، شبیهسازی جریان با عدد رینولدز بالا حول یک جسم باشد، لایه مرزی روی جسم در مقایسه با طول مشخصه جسم بسیار نازک و دارای ضخامت کم خواهد بود. اگر در این حالت جدایش جریان زیادی وجود نداشته باشد، گرادیانهای جریانی حاضر در تنشهای لزج فقط در راستای عمود بر سطح (جهت η در شکل زیر) مقدار قابل توجهی خواهند داشت و میتوان از گرادیانهای در راستای جریان (جهت ζ در شکل زیر) صرف نظر کرد.
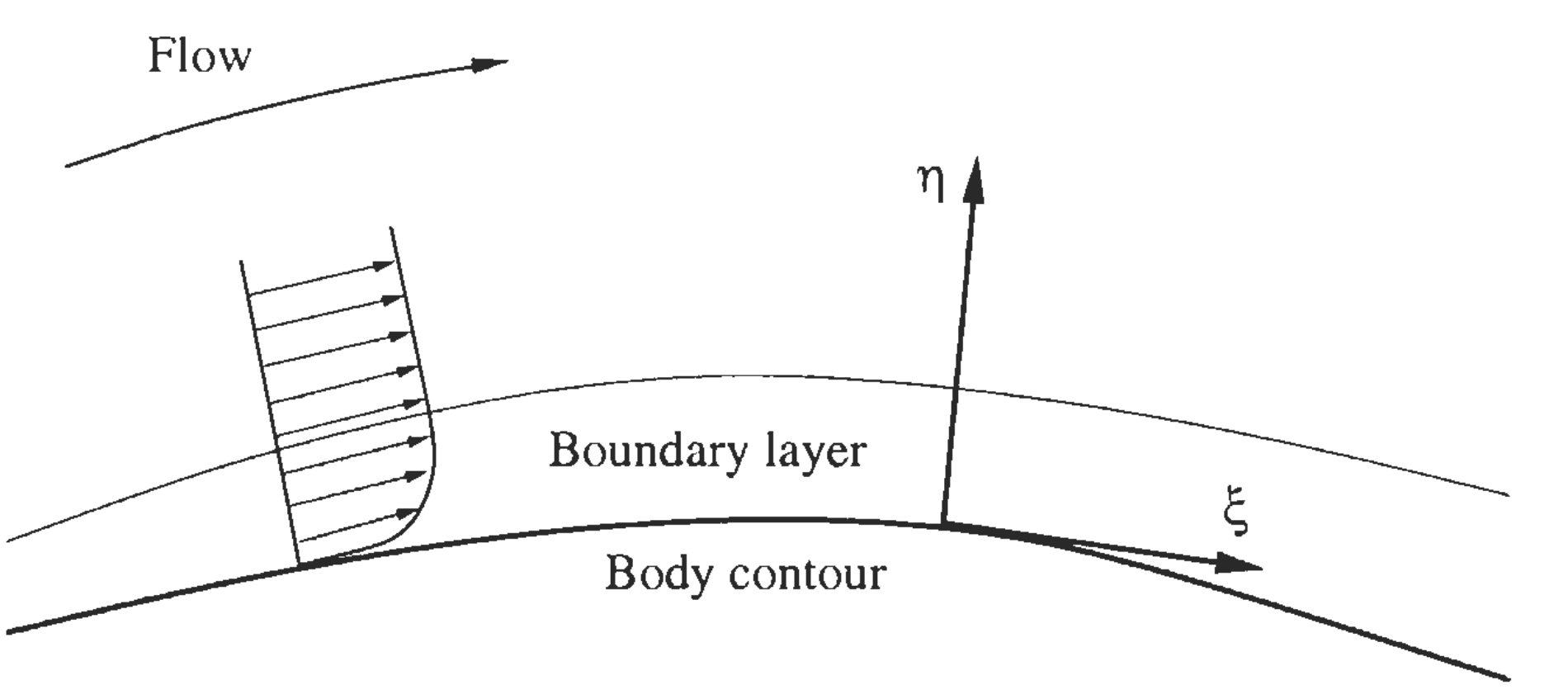
به این حالت تقریب لایه برشی نازک (Thin Shear Layer (TSL) Approximation) معادلات ناویر-استوکس میگویند. با اعمال این تقریب با وجود حفظ دقت، هزینه محاسباتی تنشهای لزج کاهش مییابد.
اگر سه شرط زیر برقرار باشد:
معادلات حاکم میتوانند به فرمPNS (Parabolised Navier-Stokes) ساده شوند. با وجود این فرضیات، مشتقهای u، v و w در جهت جریان در تنشهای لزج، کار تانسور تنش و جمله انتقال حرارت جابهجایی در جهت جریان در بردار شار لزج صفر در نظر گرفته میشوند. با این کار یک مسئله سهبعدی پیچیده تبدیل به مجموعهای از مسائل دوبعدی سادهتر و باعث صرفهجویی زیادی در هزینه محاسباتی میشود. از کاربردهای PNS میتوان به شبیهسازی جریانهای داخل مجاری و لولهها و نیز جریان فراصوتی پایا اشاره کرد [۱].
همانطور که مشاهده کردید معادلات ناویر-استوکس برای جریانهای لزج هستند. برخی اوقات مثلا برای جریانهای با عدد رینولدز بالا که ضخامت لایه مرزی در مقایسه با طول مشخصه مسئله بسیار کم باشد، میتوان کلا جمله لزجت را صفر در نظر گرفت. در این حالت:
![]()
و معادلات بهصورت زیر درمیآیند [۱]:
بنابراین میتوان گفت که معادلات حاکم بر جریان غیرلزج معادلات اویلر هستند. نسبت به معادله اویلری که قبلا معرفی شد، در معادلات بالا فرض تراکمناپذیری و ثابت بودن ضرایب لزجت اعمال نشده است.
در این مقاله بعد از بیان فرم کلی رابطه قانون بقا در دو حالت دیفرانسیلی و انتگرالی، معادلات حاکم بر جریان سیال بهصورت کامل و در فرمهای مختلف معرفی شدند. معنای فیزیکی جملات مختلف حاضر در قانون بقا بیان شدند. فرمهای سادهتر معادلات نیز ارائه شدند. شکل زیر نیز در این زمینه میتواند مفید باشد.

با دانلود فایل PDF مقاله همیشه میتوانید به این آموزش دسترسی داشته باشید.
درباره نویسنده: دانشآموخته رشته مهندسی هوافضا از دانشگاه صنعتی شریف، عضو هیئت علمی گروه مهندسی مکانیک در دانشگاه فردوسی مشهد، آموزش و پژوهش در حوزه CFD از سال ۱۳۸۵
توسط جواد سپاهی یونسی
16
اردیبهشتتوسط جواد سپاهی یونسی
15
اردیبهشتتوسط جواد سپاهی یونسی
14
اردیبهشتدانلود سریع و آسان
مطالب ما را به راحتی دانلود کنید.اساتید مجرب و حرفهای
تمام مطالب به تایید اساتید کاربلد میرسد.مطالب بهروز
مطالب منطبق بر آخرین ورژن نرمافزارها است.آموزش کاملا فارسی
تمام مطالب آموزشی به فارسی است.پشتیبانی محصولات
تمام محصولات به مدت یک ماه پشتیبانی میشوند.وبسایت CFD EXPERTS با هدف آموزش، مشاوره و انجام پروژه در حوزه CFD راهاندازی شده است. ما قصد داریم به جایگاهی برسیم که بتوانیم پاسخگوی تمام نیازهای محققان و دانشجویان در حوزه CFD باشیم. این مهم نیازمند حمایت شما کاربران عزیز است. قسمتهای جذاب و متنوعی برای CFD EXPERTS در نظر گرفته شده است که به مرور رونمایی خواهند شد. انجام فعالیتهای اصیل، دقیق و با سطح کیفی بالا و همچنین پشتیبانی منظم و مسئولانه محصولات، از مهمترین اهداف CFD EXPERTS است.
تمامی حقوق مادی و معنوی مطالب، مقالات، خودآموزها، دورهها و محصولات برای مدیریت سایت cfdexperts.net محفوظ است و کپیبرداری پیگرد قانونی دارد.
با سلام و احترام
از مطالب بسیار عالی و نکات ارزشمند حضرتعالی بسیار سپاسگزارم.
سلام. ممنونم. موفق و سلامت باشید.
سلام
بعد ده سال تصمیم به ادامه تحصیل گرفتم و برای مرور مقاله شمارو پیدا کردم. بی نهایت مفید و منسجم بود. خسته نباشید و تشکر فراوان
با سلام و احترام. خوشحالم برایتان مفید بوده است.
سالی که نکوست از بهارش پیداست.
چکیده مقاله پر از غلط است، وای به حال بقیه متن.
نوشتید معادلات ناویر استوکس شامل معادلات بقا جرم، ممنتوم و انرژی است، در حالی که کاملا غلط است.
معادلات ناویر استوکس از قانون دوم نیوتون منتج میشود. و شکل بقایی ممنتوم برای روش FVM استفاده می شود. و این دو با هم متفاوت هستند.
دوما معادلات بقا جرم ربطی به معادله ناویر استوکس ندارد زیرا این معادله بالانس بین نیرو های جابجایی و نفوذ(در حالتی که تغییرات با زمان نداریم) است.
سوما ماهیت انرژی با نیرو متفاوت است، به عنوان یک تعریف ساده انرژی نیروی است، که در راستای جابجایی دلخواه(درست) است.
با سلام و تشکر از اظهار نظر شما. برای بررسی صحت نظرات شما و بنده توصیه میکنم به کتابهای مرجع CFD در لینک زیر مراجعه کنید:
https://cfdexperts.net/download-cfd_resources/download-50-cfd-ebooks
سلام وقت بخیر..ببخشید این مقاله در ژورنال های خارجی به ثبت رسیده؟؟؟
سلام وقت شما هم بخیر. قسمت اعظم این مقاله بر اساس سه منبعی است که در انتهای مقاله ذکر شده است و نمیتوان آن را در جایی سابمیت کرد.
یعنی آنقدر خوب توضیح داده بودید که بیشتر ابهامات برام برطرف شدن
ممنونم👌😊
سلام. از لطف شما بسیار متشکرم. موفق باشید.