برای مشاهده لیست وارد شوید...
مشاهده محصولات فروشگاههیچ محصولی در سبد خرید نیست.
دینامیک سیالات محاسباتی یا CFD، شبکه محاسباتی، شبکه باسازمان، شبکه بیسازمان، شبکه غیریکنواخت، روش جبری، معیارهای Smoothness، Aspect Ratio و Skewness
فهرست مطالب |
مش باسازمان (Structured) و مش بیسازمان (Unstructured)
مش کارتزین (Cartesian) و مش منطبق بر جسم (Body-fitted)
مش یکنواخت (Uniform) و مش غیریکنواخت (Non-uniform)
دستهبندی مش بر اساس شکل سلولها/المانها
معیار ضریب منظری (Aspect Ratio)
درباره مراحل شبیهسازی جریان سیال با استفاده از CFD در این مقاله صحبت شده است. همانطور که در شکل زیر نشان داده شده است، یکی از این مراحل تولید شبکه (Grid Generation) است. هدف این مرحله تبدیل فضای فیزیکی واقعی که یک فضای پیوسته است به یک میدان حل گسسته است تا بعدا معادلات حاکم در آن میدان حل شوند. بنابراین خروجی این مرحله مختصات نقاط شبکه است. این مختصات بعدا در گسستهسازی معادلات حاکم استفاده خواهند شد.
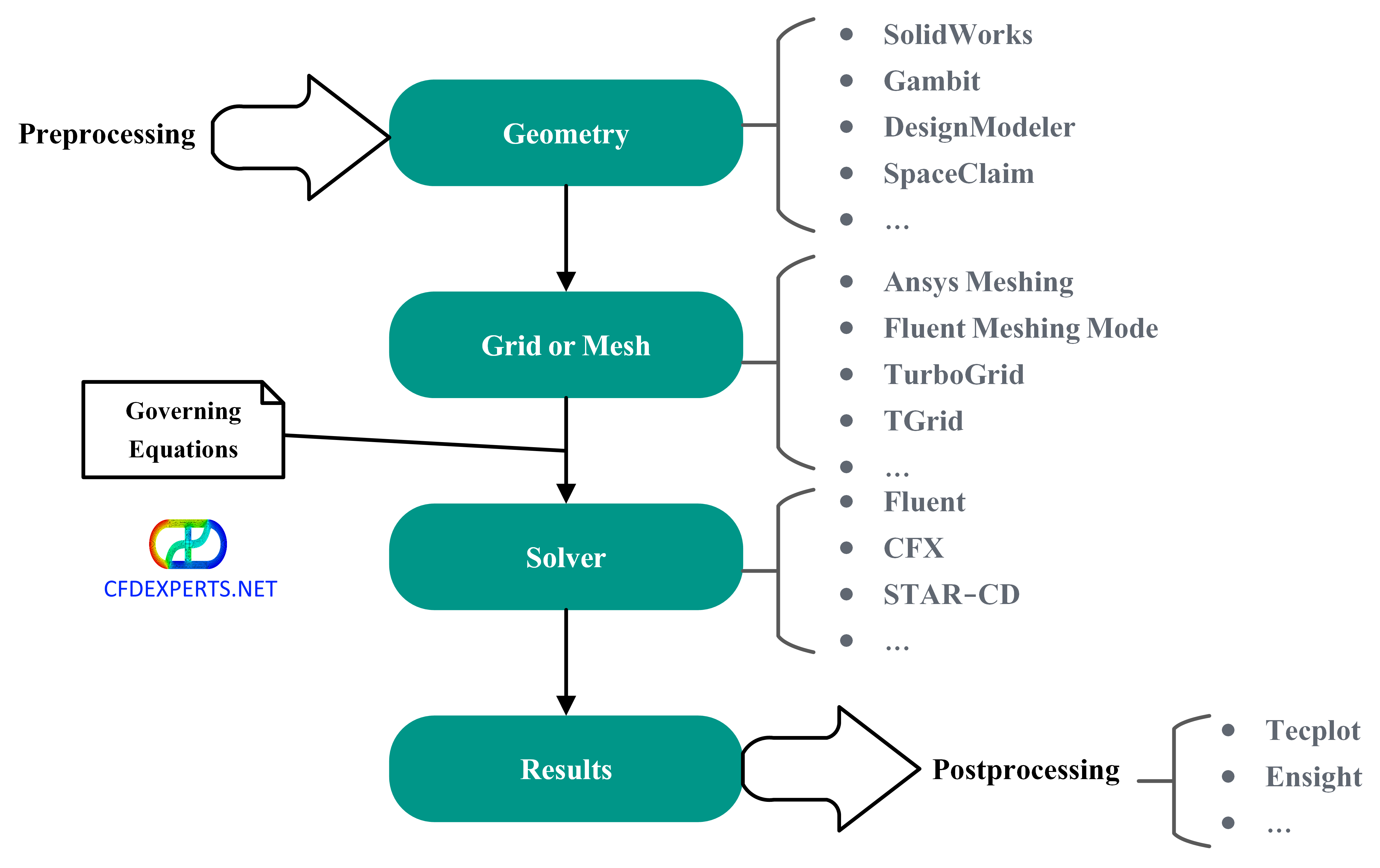
شبکه یا مش (Mesh) را از جنبههای مختلفی میتوان دستهبندی کرد. در این قسمت بهمنظور آشنایی شما با شبکه محاسباتی، دستهبندیها و انواع مختلف شبکه محاسباتی مختصرا بیان میشود.
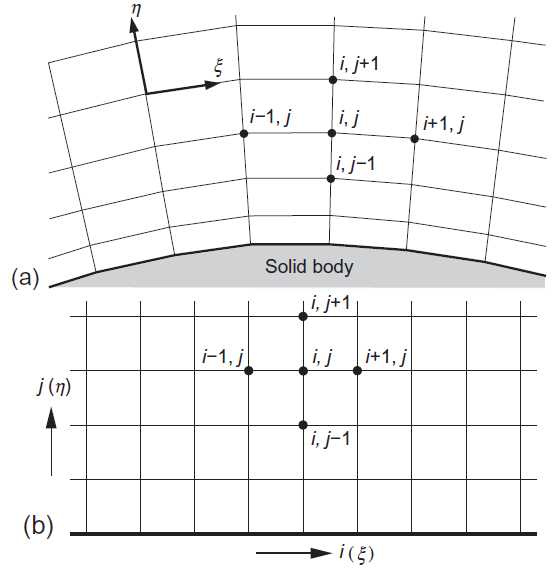
در یک نگاه کلی مش را میتوان به مش باسازمان و مش بیسازمان تقسیم کرد. همانطور که در شکل زیر نشان داده شده است، در مش باسازمان هر نقطه از شبکه که اصطلاحا Node یا Vertex نامیده میشود، بهصورت یکتا توسط اندیسهای i، jو k و مختصات کارتزین xi,j,k، yi,j,k و zi,j,k مشخص میشود [۱]. در حقیقت در این شبکه حسابوکتاب نقاط شبکه مشخص و منظم است. در این شبکه در حالت دوبعدی سلولها چهارضلعی (Quadrilateral) و در حالت سهبعدی ششوجهی (Hexahedron) هستند.
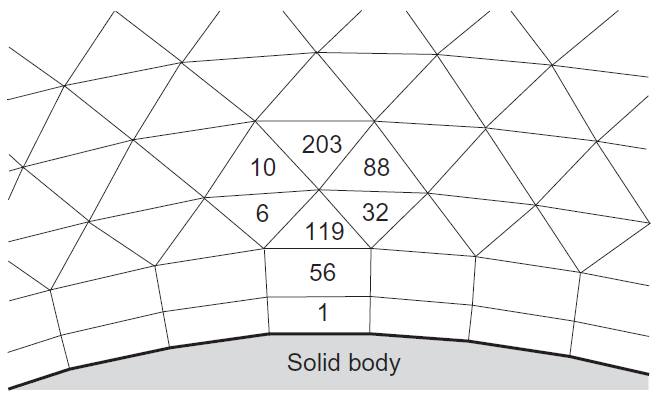
در شبکه بیسازمان سلولها و نقاط شبکه نظم و ترتیب مشخصی ندارند و نقاط یا سلولهای شبکه را نمیتوان بهصورت مستقیم توسط اندیسهایشان مشخص کرد (مثلا در شکل زیر سلول ۶ در مجاورت سلول ۱۱۹ قرار گرفته است) [۱]. در این شبکه در حالت دوبعدی سلولها مثلثی، چهارضلعی یا چندضلعی و در حالت سهبعدی چهاروجهی (Tetrahedron)، منشوری (Prism)، هرمی (Pyramid)، ششوجهی (Hexahedron) یا چندوجهی (Polyhedral) هستند [۲].
مزیت اصلی مش باسازمان این است که اندیسها یک فضای خطی و منظم تشکیل میدهند و پیدا کردن سلولها و گرههای مجاور یک سلول (بالا، پایین، چپ و راست) بسیار ساده است. درنتیجه محاسبه گرادیانها و شارهای جریان و مدلسازی لایه مرزی در این مش بسیار ساده است. اشکال اصلی این مش هم این است که تولید آن در هندسههای پیچیده مشکل است. یک راه برای رفع این مشکل این است که فضای محاسباتی به یک سری بلوک سادهتر که راحتتر مش زده میشوند، تبدیل شود که به آن شبکه Multiblock میگویند. البته یک اشکال شبکه Multiblock معاوضه اطلاعات بین بلوکها هنگام حل جریان است [۱].
مزیت اصلی مش بیسازمان این است که با استفاده از آن تولید شبکه برای هندسههای پیچیده بسیار راحتتر از مش باسازمان Multiblock است. این مزیت بر پایه این واقعیت است که سلولهای مثلثی (در حالت دوبعدی) و چهاروجهی (Tetrahedral) (در حالت سهبعدی) میتوانند بهصورت خودکار و مستقل از پیچیدگی دامنه تولید شوند. البته نباید از تولید مش با کیفیت غافل شد. برای مدلسازی صحیح لایه مرزی توصیه میشود در حالت دوبعدی از سلولهای مستطیلی و در حالت سهبعدی از سلولهای منشوریشکل یا ششوجهی در نزدیکی مرزهای جامد استفاده شود. در این حالت مش بیسازمان ترکیبی (Hybrid) خواهد بود، زیرا سلولها شکل یکسانی ندارند. باوجود اینکه تولید یک مش بیسازمان ترکیبی برای یک هندسه پیچیده در حالت کلی ساده نیست، ولی زمانی که برای تولید آن صرف میشود معمولا بسیار کمتر از زمان لازم برای تولید یک مش باسازمان Multiblock است [۱].
از معایب مش بیسازمان میتوان به ساختار پیچیده ذخیرهسازی اطلاعات نقاط شبکه و متغیرهای جریان در آن اشاره کرد که میتواند هزینه محاسباتی را افزایش دهد. البته مزیت تولید نسبتا سریع مش در هندسههای پیچیده بر این عیب میچربد. به همین خاطر است که اکثر نرمافزارهای تجاری CFD به این نوع مش تمایل بیشتری دارند [۱].
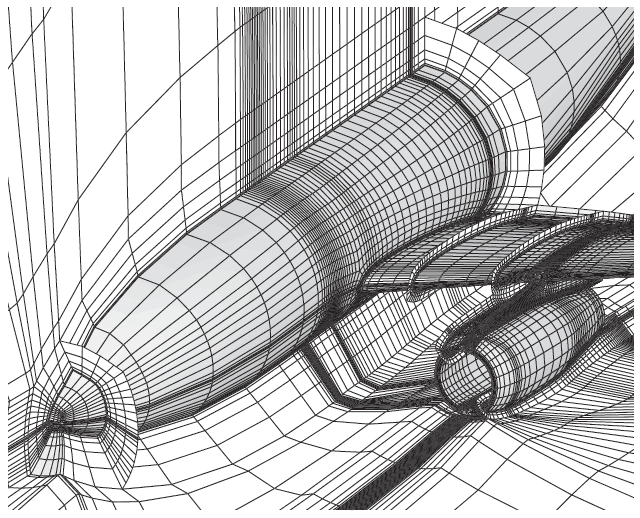
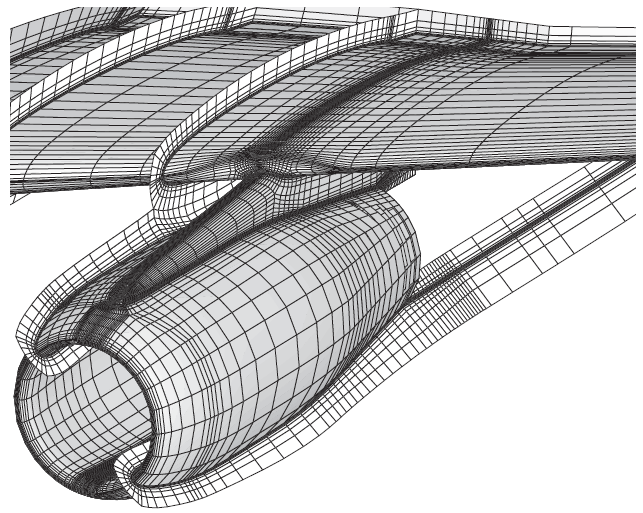
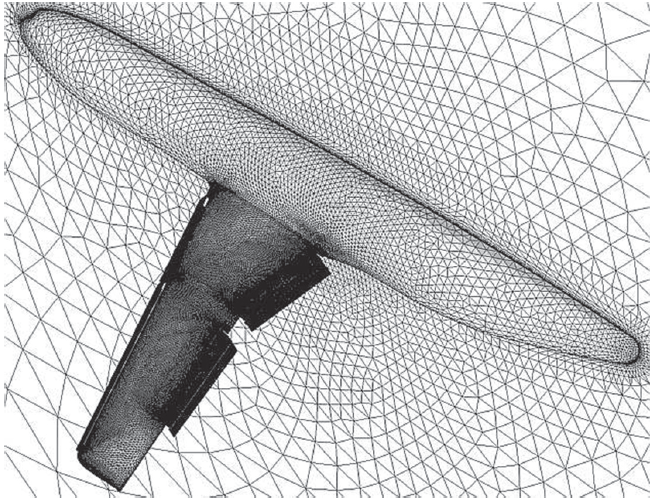
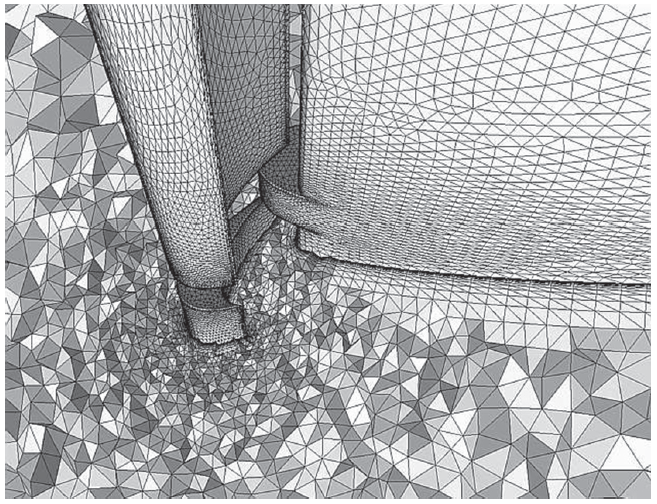
مشی که منطبق و همراستا با مرزهای دامنه حل و جسم باشد، مش منطبق بر جسم نامیده میشود [۱].
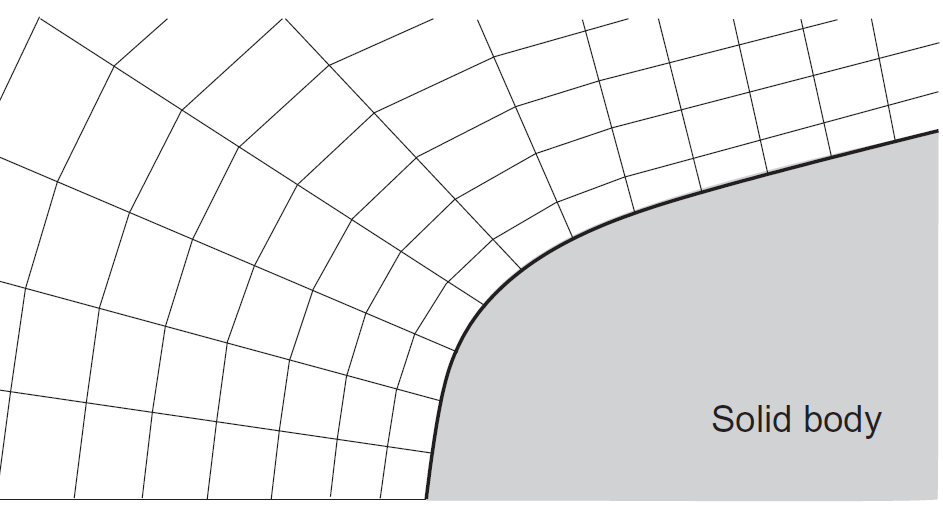
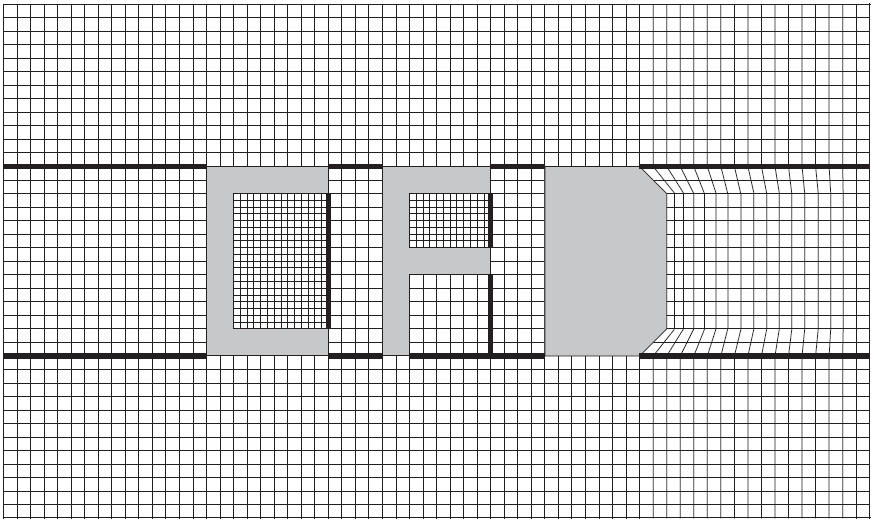
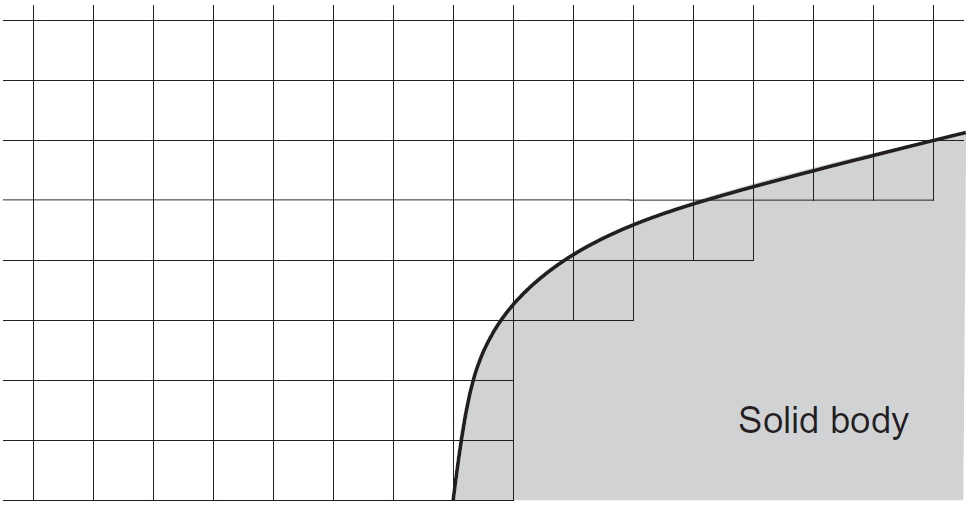
مزیت اصلی این مش این است که جریان در مجاورت مرزها با دقت بالایی محاسبه میشود و عیب اصلی آن این است که برای هندسههای واقعی تولید آن مشکل و پیچیده است. در مقابل، مش کارتزین وجود دارد که خطوط شبکه موازی با محورهای مختصات هستند و بهسادگی تولید میشود. مزیت اصلی مش کارتزین این است که محاسبه شارهای جریان در این شبکه بسیار ساده میشود. اما همانطور که شکلهای زیر نشان میدهد، مدلسازی صحیح لبهها و مرزهای دامنه و هندسه در این مش مشکل است. به همین دلیل در حالت کلی استفاده از مش منطبق بر جسم یا ترکیبی از مش کارتزین و مش منطبق بر جسم توصیه میشود [۱].
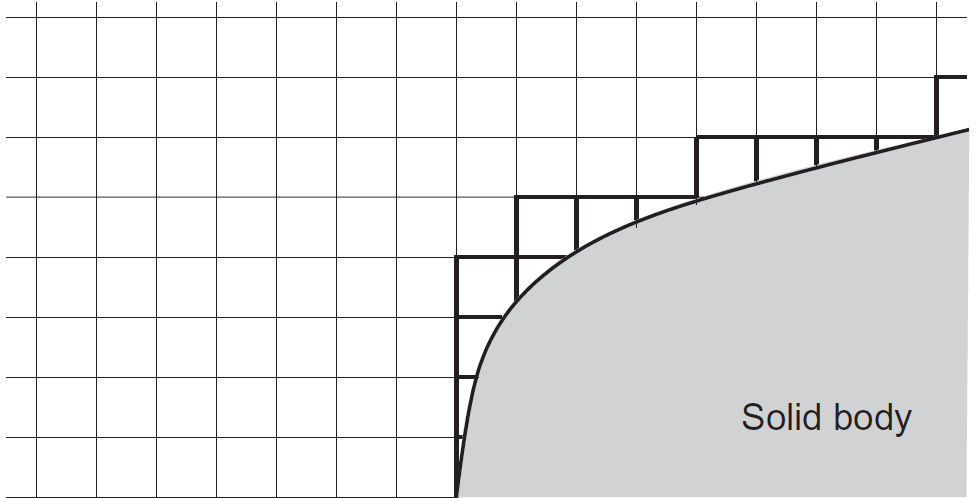
بر اساس ظاهر خطوط مش، مش منطبق بر جسم به H-type، C-type، O-type و I-type تقسیم میشود که در شکلهای زیر نشان داده شدهاند.
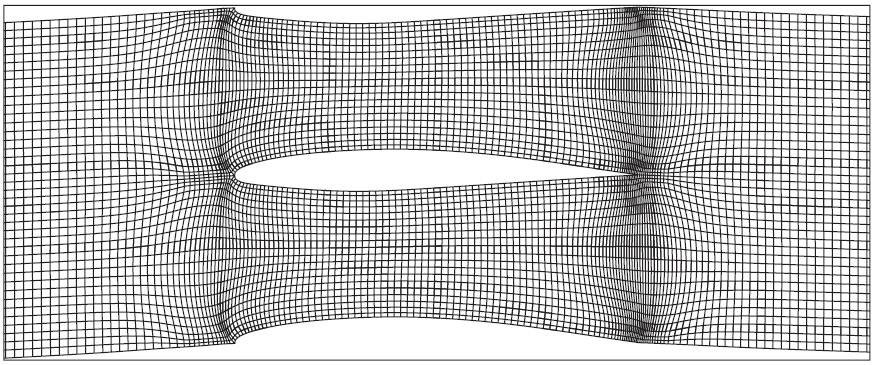
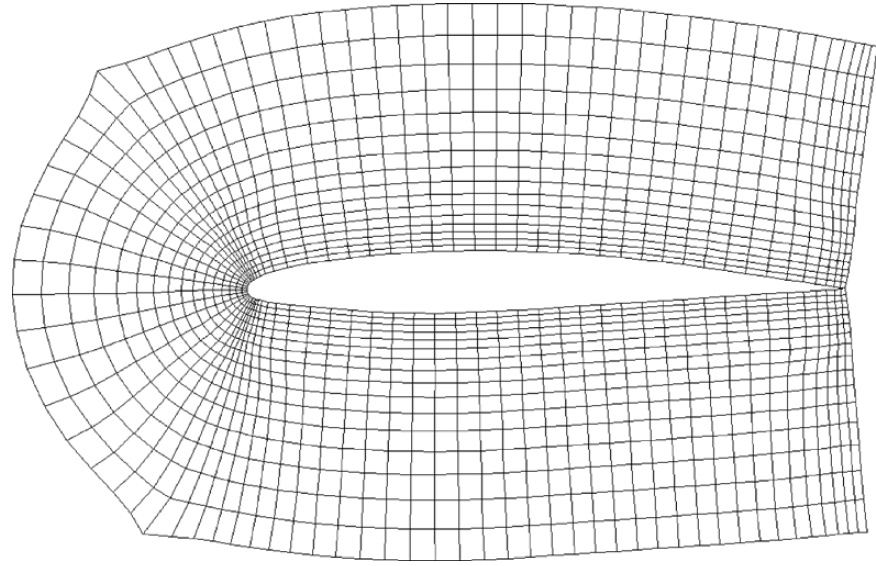
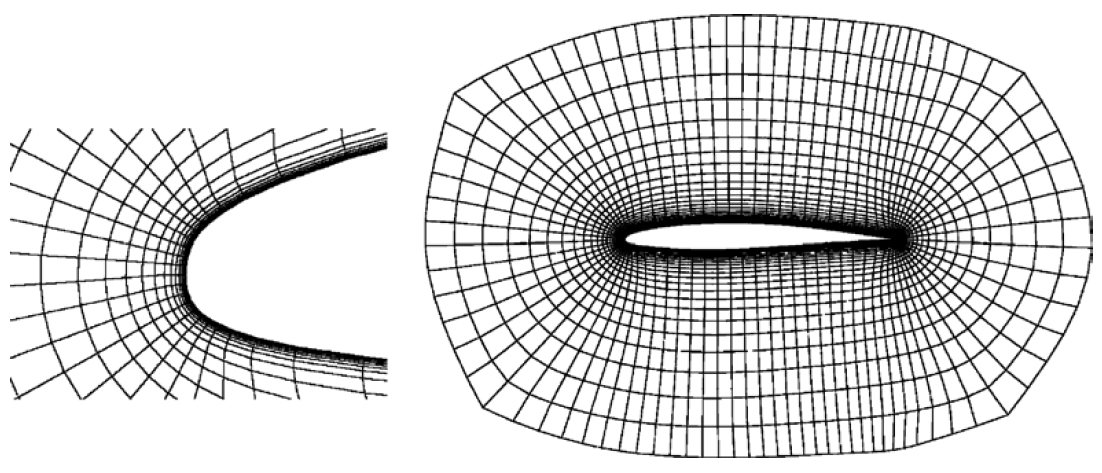
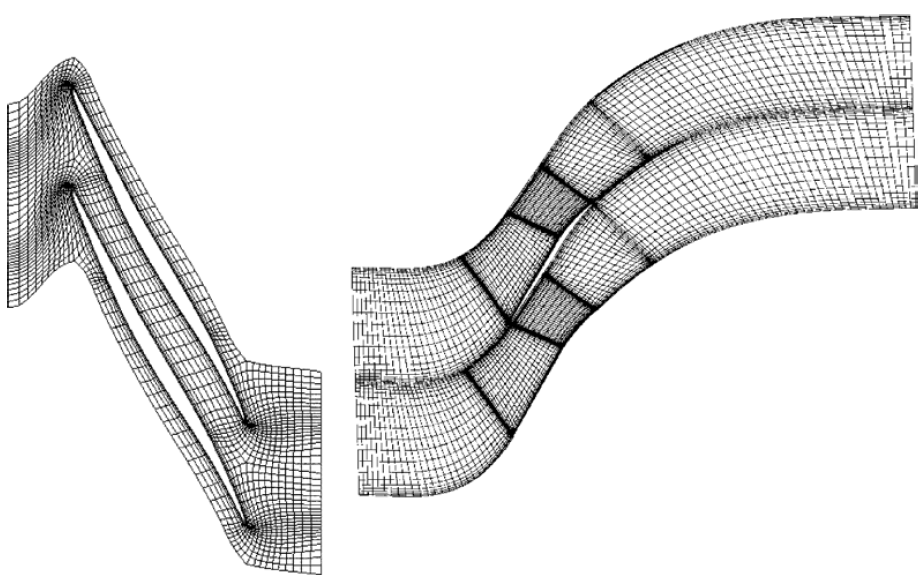
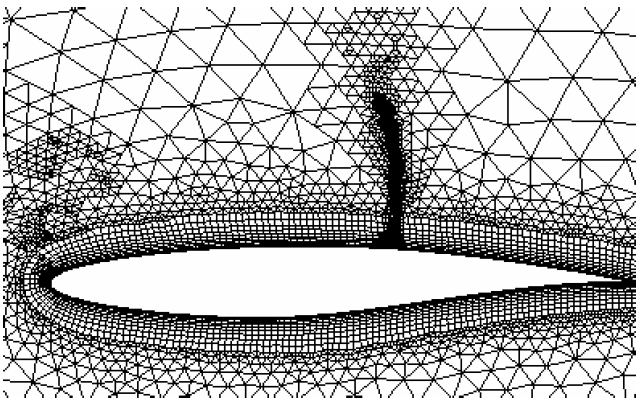
مشی یکنواخت است که اندازه سلولهای آن در تمام دامنه یکسان و بدون تغییر باشد. معمولا استفاده از مش غیریکنواخت توصیه میشود، زیرا در آن در مکانهای مورد نیاز میتوان تراکم سلولها را افزایش داد. سوالی که پیش میآید این است که کجا باید تراکم سلولها را بالا برد و اصطلاحا مش را ریز کرد. پاسخ این است که هر کجا گرادیان (تغییر شدید) وجود داشته باشد. گرادیان دو نوع است، جریانی و هندسی. لبه تیز اجسام مثالی از گرادیان هندسی است که برای مدلسازی درست آن لازم است مش اطراف لبه تیز بهاندازه کافی ریز شود. لایه مرزی، امواج ضربهای (Shock Waves) و جدایش جریان هم مثالهایی از گرادیان جریانی هستند. در شکلهای زیر مثالهایی از شبکه غیریکنواخت آمده است.
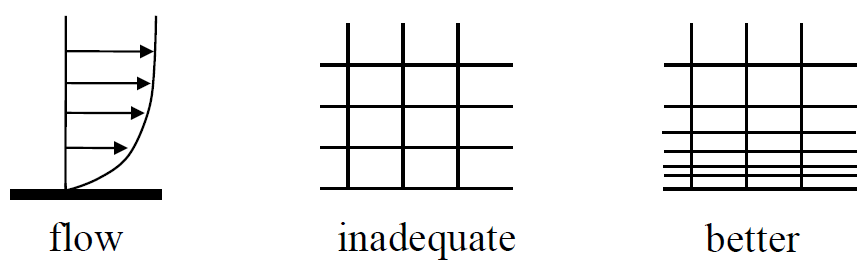

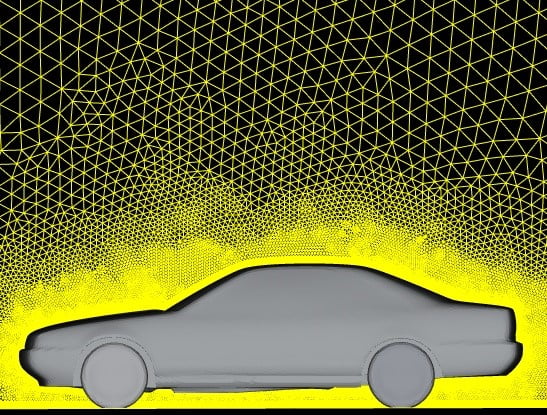
یکی از مهمترین جاهایی که لازم است در آنجا شبکه بهاندازه کافی ریز شود، لایه مرزی است. برای این کار میتوان از مش لایه مرزی (Boundary Layer Mesh) استفاده کرد. در این روش چند لایه سلول ریز که معمولا باسازمان هستند، روی دیوارههای جسم در نظر گرفته میشود تا گرادیانهای شدید جریانی موجود در داخل لایه مرزی و خصوصا در راستای عمود بر آن بهدرستی محاسبه شوند. خارج از لایه مرزی و دور از سطح جسم، از سلولهای درشتتر استفاده میشود. معمولا سلولهای موجود در مش لایه مرزی در حالت دوبعدی مستطیلی و در حالت سهبعدی منشوریشکل یا ششوجهی هستند. در شکلهای زیر چند نمونه استفاده از مش لایه مرزی نشان داده شده است.
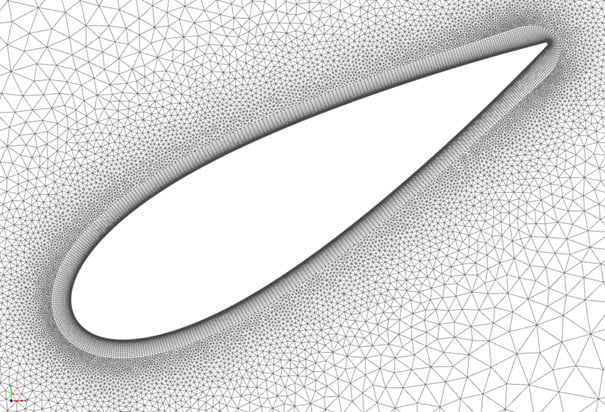
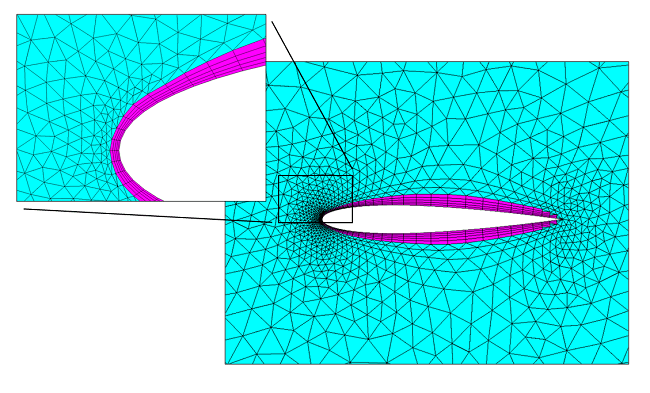

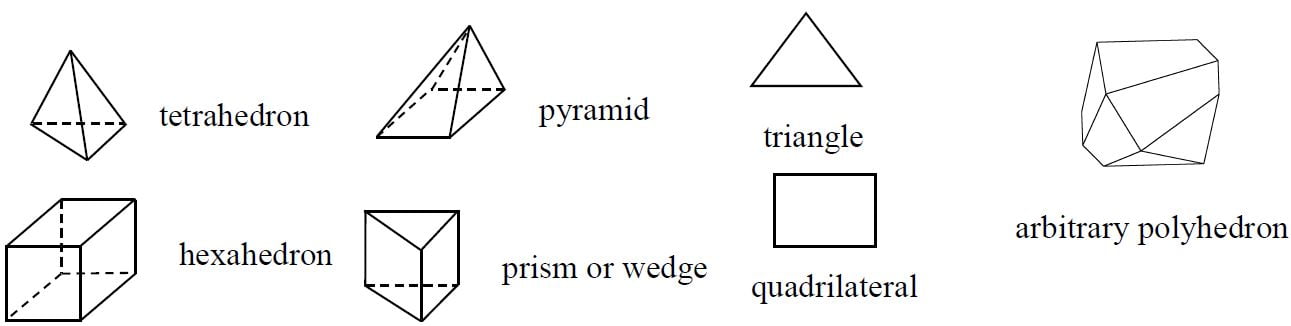
همانطور که در شکل زیر نشان داده شده است، شکلهای مختلفی برای سلولها/المانهای شبکه در دسترس است که انتخاب آنها بستگی به مسئله مورد بررسی و حلگر CFD دارد.
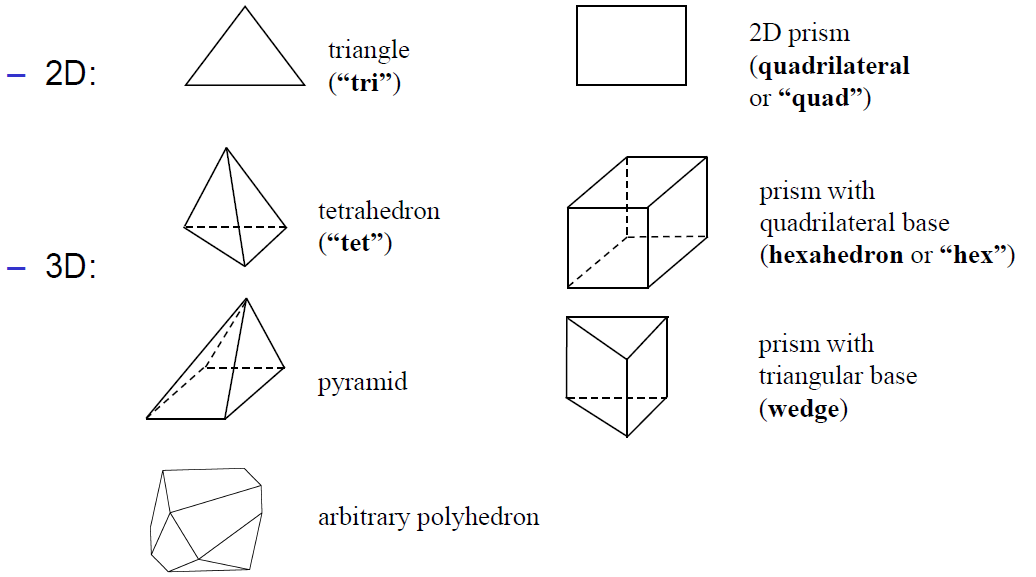
در کدها و نرمافزارهای مختلف بر اساس شکل سلولهای استفادهشده در مش، اسامی زیر ممکن است برای مش استفاده شود [۳]:
در حالت دوبعدی سلولهای آن بخشی مثلثی و بخشی چهارضلعی باشند،
در حالت سهبعدی سلولهای آن هر ترکیبی از سلولهای چهاروجهی، منشوری (Prism) یا هرمی (Pyramid) باشند،
مش لایه مرزی: در حالت سهبعدی در مجاورت دیوارهها سلولها منشوری و در سایر نقاط چهاروجهی باشند،
مش Hexcore: در حالت سهبعدی در مرکز دامنه سلولها ششوجهی و در مجاورت دیوارهها از انواع دیگر باشند،
سه روش برای تولید شبکه وجود دارد که عبارتاند از روش جبری، روش حل PDE و روش Conformal Mapping. در روش جبری که به آن روش هندسی هم میگویند، شبکه با استفاده از یک سری روابط جبری که ماهیت هندسی دارند، تولید میشود. در روش حل PDE یک سری معادله PDE که میتوانند ماهیت بیضوی، سهومی و یا هذلولوی داشته باشند، حل و بر اساس آن شبکه تولید میشود. در روش Conformal Mapping از انتقال (Transformation) استفاده میشود تا دامنه فیزیکی به دامنه محاسباتی تبدیل شود. این روش که در آن از جبر مختلط استفاده میشود، محدود به مسائل دوبعدی است.
۱. مش سطوح را تولید کن.
۲. کیفیت مش سطوح را بررسی کن. ویژگیهای یک مش خوب و ابزارهای لازم برای بررسی کیفیت مش در ادامه معرفی خواهند شد.
۳. کیفیت مش سطوح را ارتقا بده و در صورت لزوم آنها را تعمیر کن.
۴. مش حجم را تولید کن.
۵. در صورت لزوم مش را ریزتر کن.
۶. کیفیت مش حجم را بررسی کن.
۷. سلولهای نامناسب را حذف کن.
۸. مش حجم را ذخیره کن [۳].
برای بررسی کیفیت مش سه معیار اصلی وجود دارد که در این قسمت معرفی میشوند.
منظور از این معیار تغییر تدریجی اندازه سلولها در تمام جهات است. تغییر شدید در اندازه سلولها علاوه بر کاهش دقت حل میتواند باعث واگرایی آن شود.
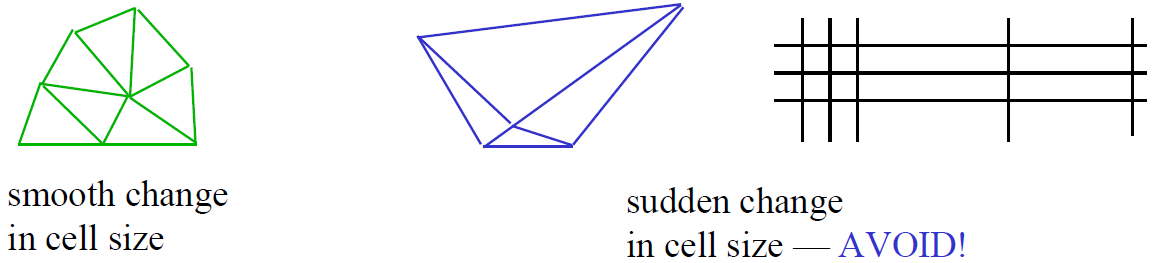
در حالت ایدهآل، بیشترین تغییر در فاصله گرهها باید کمتر از ۲۰ درصد باشد [۳].

علاوه بر پیوستگی در اندازه سلولها، دو معیار دیگر برحسب انحراف سلولها از یک سلول ایدهآل کارتزین تعریف میشود که کیفیت مش را نشان میدهند. یکی از این معیارها ضریب منظری سلول است که بهصورت نسبت بلندترین ضلع سلول به کوتاهترین ضلع آن تعریف میشود [۳]. مقدار ایدهآل آن ۱ است. مش با ضریب منظری زیاد باعث دقت کم و کند شدن نرخ همگرایی حل میشود.
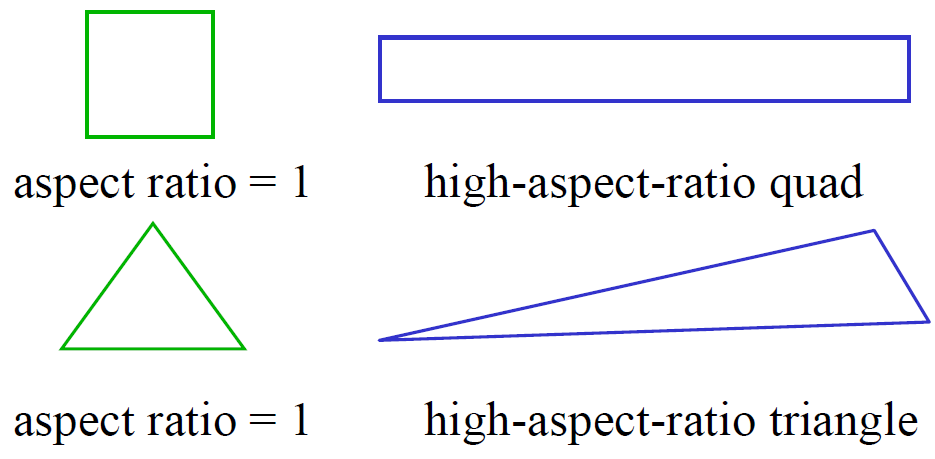
استثنائا اگر جریان توسعهیافته (Fully-developed) و ذاتا یکبعدی باشد، سلولهای quad و hex میتوانند کشیدهشده و دارای ضریب منظری بزرگتر از یک باشند [۳].

معیار دیگر برای بررسی کیفیت مش Skewness سلولها است. دو روش برای تعیین Skewness وجود دارد. روش اول بر اساس حجم سلول ایدهآل متساویالاضلاع است [۳]:
![]()
این روش فقط برای سلولهای مثلثی و چهاروجهی استفاده میشود.
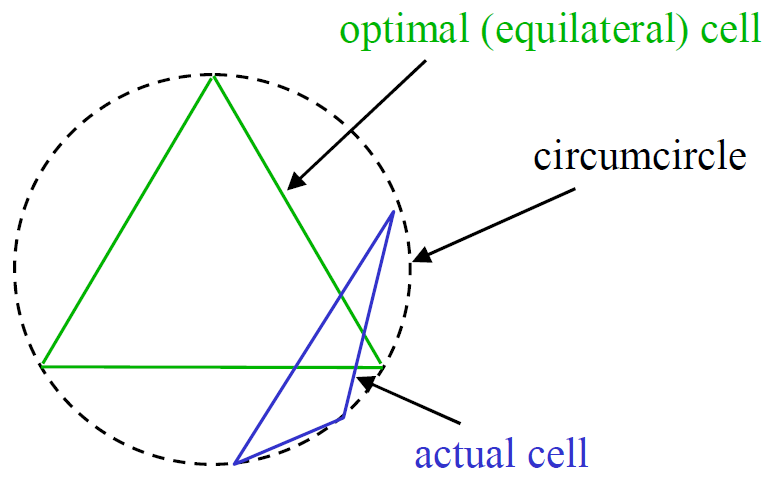
روش دوم بر اساس انحراف زاویه سلول از زاویه یک سلول متعامد است:
![]()

این روش برای هر شکلی از سلول قابل استفاده است و همیشه برای سلولهای منشوری و هرمی استفاده میشود.
رابطه اخیر برای سلول quad است. در حالت کلی:
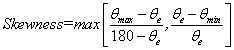
که در آن θe برای سلول quad برابر ۹۰ درجه و برای سلول مثلثی ۶۰ درجه است. به این تعریف برای Skewness بعضی اوقات Equiangle Skewness هم میگویند. محدوده Skewness بین صفر (بهترین حالت) و ۱ (بدترین حالت) است [۳].
با توجه به مباحثی که مطرح شد، اینگونه به نظر میرسد که برای تولید یک شبکه با کیفیت لازم است تعداد سلولهای شبکه بسیار زیاد و اصطلاحا مش کاملا ریز باشد. اگرچه این مطلب درست است، ولی باید توجه کرد که در کنار کیفیت مش باید به زمان و هزینه محاسباتی هم توجه کرد. ممکن است برای یک مش با تعداد سلول زیاد رایانه با سختافزار مناسب موجود نباشد و یا زمان شبیهسازی بسیار زیاد و طاقتفرسا شود. یکی از راههایی که میتوان هم مش با کیفیتی داشت و هم تعداد سلول را در حد معقول نگهداشت، اداپشن مش است. در این روش ابتدا با استفاده از یک مش نسبتا درشت یک حل اولیه از مسئله گرفته میشود. سپس بر اساس گرادیانهای جریان در حل اولیه، هر جا گرادیانها از حدی که کاربر تعریف میکند، بیشتر باشد، مش در آن نقطه ریز یا Adapt میشود (Refining). این روش اصطلاحا Solution-based Grid Adaption نام دارد. با استفاده از این روش، اگر بعد از حل اولیه مشخص شد در ناحیهای گرادیان شدیدی وجود ندارد و مش در آن ناحیه بیش از اندازه ریز شده است، میتوان مش را در آن نقطه درشت کرد (Coarsening). همچنین ریز یا درشت کردن مش علاوه بر گرادیانهای جریان میتواند بر اساس مقدار کمیتها، در راستای یک مرز و یا در یک ناحیه تعریفشده توسط کاربر باشد.

بر اساس مطالب ذکرشده در قسمتهای قبل، در ارتباط با کیفیت مش، پیشنهادهای زیر مطرح میشود:

احراز شرایط بالا در جریانها و مناطقی که گرادیان شدید وجود دارد، دارای اهمیت بیشتری میشود [۲].
شبکه باسازمان اگر تولید راحتی داشته باشد، بیشترین دقت را خواهد داشت. در مقابل شبکه بیسازمان برای هندسههای پیچیده و برای تولید خودکار مش انتخاب بهتری است. سعی شود از ناپیوستگی در اندازه سلولها، سلولهای با ضریب منظری و Skewness بالا خصوصا در نواحی با گرادیان بالا اجتناب شود. همچنین لازم است شبکه در نواحی دارای گرادیان بالا بهاندازه کافی ریز شود. استفاده از مش لایه مرزی در مجاورت دیوارهها برای مدلسازی دقیق لایه مرزی توصیه میشود.
هنگامی که جریان در حالت کلی همراستا با مرزهای هندسه است، شبکه باسازمان انتخاب مناسبی است، زیرا یک سری از خطوط شبکه در راستای خطوط جریان خواهند بود. از لحاظ دقت و هزینه محاسباتی، شبکه باسازمان بر شبکه بیسازمان ارجحیت دارد. البته تولید شبکه Multiblock باسازمان برای هندسههای پیچیده در مقایسه با شبکه بیسازمان سخت و زمانبر است.
نظرات خود را در مورد این مقاله با ما در میان بگذارید.

با دانلود فایل PDF مقاله همیشه میتوانید به این آموزش دسترسی داشته باشید.
درباره نویسنده: دانشآموخته رشته مهندسی هوافضا از دانشگاه صنعتی شریف، عضو هیئت علمی گروه مهندسی مکانیک در دانشگاه فردوسی مشهد، آموزش و پژوهش در حوزه CFD از سال ۱۳۸۵
توسط جواد سپاهی یونسی
16
اردیبهشتتوسط جواد سپاهی یونسی
16
اردیبهشتتوسط جواد سپاهی یونسی
15
اردیبهشتتوسط جواد سپاهی یونسی
14
اردیبهشتدانلود سریع و آسان
مطالب ما را به راحتی دانلود کنید.اساتید مجرب و حرفهای
تمام مطالب به تایید اساتید کاربلد میرسد.مطالب بهروز
مطالب منطبق بر آخرین ورژن نرمافزارها است.آموزش کاملا فارسی
تمام مطالب آموزشی به فارسی است.پشتیبانی محصولات
تمام محصولات به مدت یک ماه پشتیبانی میشوند.وبسایت CFD EXPERTS با هدف آموزش، مشاوره و انجام پروژه در حوزه CFD راهاندازی شده است. ما قصد داریم به جایگاهی برسیم که بتوانیم پاسخگوی تمام نیازهای محققان و دانشجویان در حوزه CFD باشیم. این مهم نیازمند حمایت شما کاربران عزیز است. قسمتهای جذاب و متنوعی برای CFD EXPERTS در نظر گرفته شده است که به مرور رونمایی خواهند شد. انجام فعالیتهای اصیل، دقیق و با سطح کیفی بالا و همچنین پشتیبانی منظم و مسئولانه محصولات، از مهمترین اهداف CFD EXPERTS است.
تمامی حقوق مادی و معنوی مطالب، مقالات، خودآموزها، دورهها و محصولات برای مدیریت سایت cfdexperts.net محفوظ است و کپیبرداری پیگرد قانونی دارد.
نظرات کاربران